3.如图所示的“钻石”型网格(由边长都为1个单位长度的等边三角形组成),其中已经涂黑了3个小三角形(阴影部分表示),请你再只涂黑一个小三角形,使它与阴影部分合起来所构成的图形是一个轴对称图形,则选择的方法有(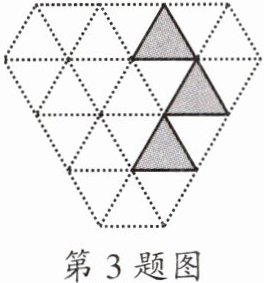
A.1种
B.2种
C.3种
D.4种
C
)
A.1种
B.2种
C.3种
D.4种
答案:
【解析】:本题考查轴对称图形的性质,根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴。
本题中,只有当涂黑的小三角形与已有的阴影部分小三角形关于某条直线对称时,所构成的图形才是轴对称图形。
观察图形可知,分别以三个阴影部分小三角形组成的图形的对称轴为对称轴,在对应的对称位置上涂黑一个小三角形,都可以得到轴对称图形,这样的对称轴有$3$条,所以选择的方法有$3$种。
【答案】:C。
本题中,只有当涂黑的小三角形与已有的阴影部分小三角形关于某条直线对称时,所构成的图形才是轴对称图形。
观察图形可知,分别以三个阴影部分小三角形组成的图形的对称轴为对称轴,在对应的对称位置上涂黑一个小三角形,都可以得到轴对称图形,这样的对称轴有$3$条,所以选择的方法有$3$种。
【答案】:C。
4.如图,在3×3的正方形网格中,从空白的小正方形中再选择一个涂黑,使得3个涂黑的正方形成轴对称图形,则选择的方法有(
A.3种
B.2种
C.3种
D.4种
D
)A.3种
B.2种
C.3种
D.4种
答案:
解:根据轴对称图形的定义,分以下情况分析:
1. 沿水平方向对称轴(中间横线):需在第二行中间格涂黑,对称。
2. 沿竖直方向对称轴(中间竖线):需在第一行中间格涂黑,对称。
3. 沿左上角到右下角对角线:需在第一行第一格涂黑,对称。
4. 沿右上角到左下角对角线:需在第一行第三格涂黑,对称。
共4种方法。
答案:D
1. 沿水平方向对称轴(中间横线):需在第二行中间格涂黑,对称。
2. 沿竖直方向对称轴(中间竖线):需在第一行中间格涂黑,对称。
3. 沿左上角到右下角对角线:需在第一行第一格涂黑,对称。
4. 沿右上角到左下角对角线:需在第一行第三格涂黑,对称。
共4种方法。
答案:D
例3 如图,小明从平面镜里看到镜子对面电子钟示数的像如图所示,这时的实际时刻应该是(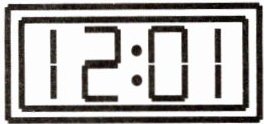
A.21:10
B.10:21
C.10:51
D.12:01
分析:根据镜子中的像与实际时刻轴对称的规律,只要在右(或左)边画一条直线作为对称轴,然后画出各数字的对称图形,这时对称图形上显示出来的就是实际时刻,如图.
归纳:
(1)若镜子里是题目中这样的数字电子钟,则使用对称的方式获取正确时间,也可以从纸的背面看;若镜子里是指针式时钟,可用对称的方式或从背面看,也可以用12减去从镜子里看到的时间,均可获得实际时间.
(2)当物体与镜面平行时,(影像与物体相比较)上下不变,左右改变;当物体与镜面垂直时,(影像与物体相比较)上下改变,左右不变.
C
)
A.21:10
B.10:21
C.10:51
D.12:01
分析:根据镜子中的像与实际时刻轴对称的规律,只要在右(或左)边画一条直线作为对称轴,然后画出各数字的对称图形,这时对称图形上显示出来的就是实际时刻,如图.

归纳:
(1)若镜子里是题目中这样的数字电子钟,则使用对称的方式获取正确时间,也可以从纸的背面看;若镜子里是指针式时钟,可用对称的方式或从背面看,也可以用12减去从镜子里看到的时间,均可获得实际时间.
(2)当物体与镜面平行时,(影像与物体相比较)上下不变,左右改变;当物体与镜面垂直时,(影像与物体相比较)上下改变,左右不变.
答案:
解:根据镜面对称规律,镜子中的像与实际时刻关于竖直直线对称,左右互换。
镜子中显示的像为“12:01”,将各数字左右对称后,得到实际时刻为“10:51”。
答案:C
镜子中显示的像为“12:01”,将各数字左右对称后,得到实际时刻为“10:51”。
答案:C
5.如图所示是汽车牌照在水中的倒影,则该车牌照上的数字是
21678
.
答案:
5. 21678
6.星期天小华去书店买书时,从镜子内看到背后墙上普通时钟的时针(粗)与分针(细)的位置如图所示,此时时钟表示的时间是
1
时30
分.(按12小时制填写)
答案:
解:根据镜面对称的性质,镜子中的时钟与实际时钟关于镜面对称,即左右方向相反。
观察镜子中的时钟,时针在10和11之间,分针指向6(即30分)。由于镜面对称左右相反,实际时针应在1和2之间,分针仍指向6(30分)。
此时时钟表示的时间是1时30分。
1;30
观察镜子中的时钟,时针在10和11之间,分针指向6(即30分)。由于镜面对称左右相反,实际时针应在1和2之间,分针仍指向6(30分)。
此时时钟表示的时间是1时30分。
1;30
1. 点 $ P(x,y) $ 关于 $ x $ 轴对称的点的坐标为 $ P_1 $(
$x$
,$-y$
).
答案:
【解析】:
本题考查了关于$x$轴对称的点的坐标性质。
根据关于$x$轴对称的点的坐标性质,如果点$P(x,y)$关于$x$轴对称,那么它的对称点$P_1$的横坐标不变,纵坐标变为相反数。
即,如果点$P$的坐标为$(x,y)$,那么它关于$x$轴对称的点$P_1$的坐标为$(x,-y)$。
【答案】:
$x$;$-y$
本题考查了关于$x$轴对称的点的坐标性质。
根据关于$x$轴对称的点的坐标性质,如果点$P(x,y)$关于$x$轴对称,那么它的对称点$P_1$的横坐标不变,纵坐标变为相反数。
即,如果点$P$的坐标为$(x,y)$,那么它关于$x$轴对称的点$P_1$的坐标为$(x,-y)$。
【答案】:
$x$;$-y$
2. 点 $ P(x,y) $ 关于 $ y $ 轴对称的点的坐标为 $ P_2 $(
$-x$
,$y$
).
答案:
【解析】:
本题考查的是关于$y$轴对称的点的坐标性质。在平面直角坐标系中,任意一点$P(x,y)$关于$y$轴对称的点$P_2$的坐标可以通过改变$x$坐标的符号得到,即$P_2(-x,y)$。这是因为关于$y$轴对称的两点,其横坐标互为相反数,而纵坐标保持不变。
【答案】:
$-x$;$y$。
本题考查的是关于$y$轴对称的点的坐标性质。在平面直角坐标系中,任意一点$P(x,y)$关于$y$轴对称的点$P_2$的坐标可以通过改变$x$坐标的符号得到,即$P_2(-x,y)$。这是因为关于$y$轴对称的两点,其横坐标互为相反数,而纵坐标保持不变。
【答案】:
$-x$;$y$。
例 1 填空题
(1) 和点 $ P(-3,2) $ 关于 $ y $ 轴对称的点的坐标是
(2) 若 $ A(a-1,3) $, $ B(4,b-2) $ 关于 $ x $ 轴对称,则 $ a= $
(3) 如图,已知点 $ A(-5,5) $, $ B(5,5) $, $ C(-1,2) $, $ D(1,2) $, $ E(-3,1) $, $ F(3,1) $ 是平面直角坐标系内的 6 个点,选择其中三个点连成一个三角形,剩下三个点连成另一个三角形.若这两个三角形关于 $ y $ 轴对称,就称为一组对称三角形,那么,平面直角坐标系中可找出
(1) 和点 $ P(-3,2) $ 关于 $ y $ 轴对称的点的坐标是
$(3,2)$
.(2) 若 $ A(a-1,3) $, $ B(4,b-2) $ 关于 $ x $ 轴对称,则 $ a= $
$5$
, $ b= $$-1$
;若关于 $ y $ 轴对称,则 $ a= $$-3$
, $ b= $$5$
.(3) 如图,已知点 $ A(-5,5) $, $ B(5,5) $, $ C(-1,2) $, $ D(1,2) $, $ E(-3,1) $, $ F(3,1) $ 是平面直角坐标系内的 6 个点,选择其中三个点连成一个三角形,剩下三个点连成另一个三角形.若这两个三角形关于 $ y $ 轴对称,就称为一组对称三角形,那么,平面直角坐标系中可找出
$3$
组对称三角形.
答案:
【解析】:
(1) 对于点 $P(x,y)$,其关于 $y$ 轴对称的点的坐标为 $P'(-x,y)$。
因此,点 $P(-3,2)$ 关于 $y$ 轴对称的点的坐标是 $(3,2)$。
(2) 当点 $A(a-1,3)$ 和 $B(4,b-2)$ 关于 $x$ 轴对称时,它们的横坐标相等,纵坐标互为相反数。
即 $a-1=4$,$b-2=-3$。
解这两个方程,得到 $a=5$,$b=-1$。
当点 $A(a-1,3)$ 和 $B(4,b-2)$ 关于 $y$ 轴对称时,它们的纵坐标相等,横坐标互为相反数。
即 $a-1=-4$,$b-2=3$。
解这两个方程,得到 $a=-3$,$b=5$。
(3) 观察给定的六个点 $A(-5,5)$,$B(5,5)$,$C(-1,2)$,$D(1,2)$,$E(-3,1)$,$F(3,1)$,可以发现它们关于 $y$ 轴对称。
因此,可以形成以下三对关于 $y$ 轴对称的三角形:
$\triangle ACE$ 与 $\triangle BDF$;
$\triangle ADE$ 与 $\triangle BCF$;
$\triangle ACF$ 与 $\triangle BDE$。
但需要注意 $A$,$D$,$F$ 三点与 $B$,$C$,$E$ 三点分别共线,不构成三角形。
所以,可找出 4-1=3 组对称三角形(除去共线的情况)。
【答案】:
(1) $(3,2)$;
(2) $5$;$-1$;$-3$;$5$;
(3) $3$。
(1) 对于点 $P(x,y)$,其关于 $y$ 轴对称的点的坐标为 $P'(-x,y)$。
因此,点 $P(-3,2)$ 关于 $y$ 轴对称的点的坐标是 $(3,2)$。
(2) 当点 $A(a-1,3)$ 和 $B(4,b-2)$ 关于 $x$ 轴对称时,它们的横坐标相等,纵坐标互为相反数。
即 $a-1=4$,$b-2=-3$。
解这两个方程,得到 $a=5$,$b=-1$。
当点 $A(a-1,3)$ 和 $B(4,b-2)$ 关于 $y$ 轴对称时,它们的纵坐标相等,横坐标互为相反数。
即 $a-1=-4$,$b-2=3$。
解这两个方程,得到 $a=-3$,$b=5$。
(3) 观察给定的六个点 $A(-5,5)$,$B(5,5)$,$C(-1,2)$,$D(1,2)$,$E(-3,1)$,$F(3,1)$,可以发现它们关于 $y$ 轴对称。
因此,可以形成以下三对关于 $y$ 轴对称的三角形:
$\triangle ACE$ 与 $\triangle BDF$;
$\triangle ADE$ 与 $\triangle BCF$;
$\triangle ACF$ 与 $\triangle BDE$。
但需要注意 $A$,$D$,$F$ 三点与 $B$,$C$,$E$ 三点分别共线,不构成三角形。
所以,可找出 4-1=3 组对称三角形(除去共线的情况)。
【答案】:
(1) $(3,2)$;
(2) $5$;$-1$;$-3$;$5$;
(3) $3$。
查看更多完整答案,请扫码查看


