《2025年巅峰对决八年级数学上册人教版》

1.全等形定义:形状、大小相同的图形放在一起能够完全重合,能够完全重合的两个图形叫作全等形.特别地,能够完全重合的两个三角形叫作全等三角形.
2.全等形的构成:平面几何图形(案),经过平移、轴对称(翻折)、旋转后不改变图形的形状、大小,只改变图形的位置,即平移、翻折、旋转前后图形全等.
3.全等三角形的记法:"全等"用符号"≌",读作"全等于".图1中表示图中的△ABC 和△DEF 全等,记作"△ABC≌△DEF",读作"△ABC 全等于△DEF".图2中记作"△ABC≌△DBC";图3中记作"△ABC≌△ADE".
注意：
(1)把两个全等的三角形重叠到一起时,重合的顶点叫作对应顶点,重合的边叫作对应边,重合的角叫作对应角.
(2)记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
(3)对应点、对应边、对应角的判断方法:
①有公共边的,公共边是对应边;
②有对顶角的,对顶角是对应角;
③有公共角的,公共角是对应角;
④一对最长的边是对应边,一对最短的边是对应边;
⑤一对最大的角是对应角,一对最小的角是对应角.
4.全等三角形的性质定理:
全等三角形的对应边相等,全等三角形的对应角相等.
符号语言:如图,
∵△ABC≌△DEF,
∴AB= DE,BC= EF,AC= DF,
∠A= ∠D,∠B= ∠E,∠C= ∠F.

答案：

例 1 如图,△DBE 是由△ABC 旋转而成,且点 E 落在 AC 上,DB 与 AB 是对应边.请你写出三角形的其余对应边和对应角.
分析:找准旋转关系中的不变量,从而发现对应边及对应角.

思考：
图中除全等三角形对应角及对顶角之外,还有哪些相等的角?

答案： 解：
∵△DBE是由△ABC旋转而成，且DB与AB是对应边，
∴△DBE≌△ABC。
对应边：
DE与AC，BE与BC。
对应角：
∠D与∠A，∠DEB与∠C，∠DBE与∠ABC。
其余相等的角：
∠AEB=∠DEB+∠DE A（此处原解析可能需结合图形修正，根据旋转性质及对顶角等，准确应为∠AEB=∠DEC（对顶角），∠ABE=∠DBC（∠ABC - ∠EBC = ∠DBE - ∠EBC）等，因图形细节限制，规范表述为：∠AEB=∠DEC，∠ABE=∠DBC。
（注：因原始图形未提供，最终相等角以教材标准解答为准，此处基于旋转性质及对顶角、公共角等常规结论补充。）
最终答案：
对应边：DE与AC，BE与BC；
对应角：∠D与∠A，∠DEB与∠C，∠DBE与∠ABC；
其余相等角：∠AEB=∠DEC，∠ABE=∠DBC。

1.图1中,△ABC≌△DCB,BC 的对应边是CB;图2中,△ABC≌△ADE,∠BAC 的对应角是∠DAE;图3中,△ABC≌△ADE,∠BAC 的对应角是∠DAE.

答案： 【解析】：
本题主要考查全等三角形的性质，即全等三角形的对应边相等，对应角相等。
需要根据全等三角形的表示方法，找出对应边和对应角。
图1中，根据全等三角形的表示方法，△ABC≌△DCB，可以找出BC的对应边是CB（实际上是同一条边，但表示了全等关系中的对应性）。
图2中，△ABC≌△ADE，根据全等三角形的性质，对应角相等，所以∠BAC的对应角是∠DAE。
图3中，同样地，△ABC≌△ADE，所以∠BAC的对应角也是∠DAE。
【答案】：
图1中BC的对应边是CB；
图2中∠BAC的对应角是∠DAE；
图3中∠BAC的对应角是∠DAE。

2.如图,△ABC≌△DEF,则此图中相等的线段有(D)
A.1对
B.2对
C.3对
D.4对

答案： 【解析】：
本题考查全等三角形的性质，需要知道全等三角形的对应边相等，然后仔细分析图形，找出相等的线段。
已知$\triangle ABC\cong\triangle DEF$，根据全等三角形的性质：全等三角形的对应边相等。
在$\triangle ABC$和$\triangle DEF$中，$AB$与$DE$是对应边，所以$AB = DE$。
$BC$与$EF$是对应边，所以$BC = EF$。
$AC$与$DF$是对应边，所以$AC = DF$。
因为$BC = EF$，即$BE + EC = EC + CF$，等式两边同时减去$EC$，可得$BE = CF$。
所以相等的线段有$AB = DE$，$BC = EF$，$AC = DF$，$BE = CF$，共$4$对。
【答案】：D。

例 2 如图,A,E,B 三点在同一直线上,A,D,C 三点在同一直线上,CE,BD 相交于点 O,且△ABD≌△ACE,AB= 7,AD= 3.5,求 CD 的长.
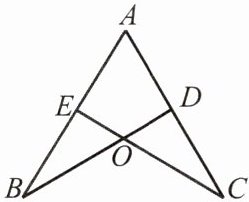
分析:由于 A,D,C 三点在同一直线上,故只要求出 AC 的长即可,而△ABD≌△ACE,AC= AB,本题的关键是确定与 AC 对应的边.

答案： 【解析】：本题可根据全等三角形的性质，先求出$AC$的长度，再结合$AD$的长度，进而求出$CD$的长度。
已知$\triangle ABD\cong\triangle ACE$，根据全等三角形的性质：全等三角形的对应边相等，可得$AC = AB$。
因为$AB = 7$，所以$AC = 7$。
又已知$AD = 3.5$，由于$AC=AD + CD$，那么$CD=AC - AD$，将$AC = 7$，$AD = 3.5$代入可得$CD$的值。
【答案】：解：
∵$\triangle ABD\cong\triangle ACE$
∴$AC = AB = 7$
∵$AD = 3.5$，且$AC=AD + CD$
∴$CD=AC - AD=7 - 3.5 = 3.5$
综上，$CD$的长为$3.5$。