4.如图,在x轴、y轴上分别截取OA,OB,使OA= OB,再分别以点A,B为圆心,以大于$\frac{1}{2}AB$的长为半径画弧,两弧交于点P.若点P的坐标为(a,2a-3),则a的值为___
1或3
.
答案:
解:由题意知,点P在∠AOB的平分线上。
∵∠AOB是直角,
∴点P到x轴和y轴的距离相等。
∵点P的坐标为(a,2a-3),
∴|a|=|2a-3|。
分两种情况:
①当a=2a-3时,解得a=3;
②当a=-(2a-3)时,a=-2a+3,3a=3,解得a=1。
综上,a的值为1或3。
∵∠AOB是直角,
∴点P到x轴和y轴的距离相等。
∵点P的坐标为(a,2a-3),
∴|a|=|2a-3|。
分两种情况:
①当a=2a-3时,解得a=3;
②当a=-(2a-3)时,a=-2a+3,3a=3,解得a=1。
综上,a的值为1或3。
一、全等形及全等三角形
1.定义:能够完全
能够完全
全等符号是
2.全等三角形的性质:
1.定义:能够完全
重合
的两个图形叫作全等形.能够完全
重合
的两个三角形叫作全等三角形.全等符号是
$\cong$
.2.全等三角形的性质:
全等三角形的对应边相等,对应角也相等
.
答案:
【解析】:
本题考查全等形及全等三角形的定义和性质。
首先,需要理解全等形的定义,即两个图形能够完全重合,则这两个图形被称为全等形。对于三角形来说,如果两个三角形能够完全重合,则它们被称为全等三角形。全等符号用“$\cong$”表示。
其次,全等三角形有一些重要的性质。根据全等三角形的定义,如果两个三角形全等,那么它们的对应边相等,对应角也相等。这是全等三角形的基本性质,也是解答此题的关键。
【答案】:
1. 定义:能够完全重合的两个图形叫作全等形。能够完全重合的两个三角形叫作全等三角形。全等符号是“$\cong$”。
2. 全等三角形的性质:全等三角形的对应边相等,对应角也相等。
本题考查全等形及全等三角形的定义和性质。
首先,需要理解全等形的定义,即两个图形能够完全重合,则这两个图形被称为全等形。对于三角形来说,如果两个三角形能够完全重合,则它们被称为全等三角形。全等符号用“$\cong$”表示。
其次,全等三角形有一些重要的性质。根据全等三角形的定义,如果两个三角形全等,那么它们的对应边相等,对应角也相等。这是全等三角形的基本性质,也是解答此题的关键。
【答案】:
1. 定义:能够完全重合的两个图形叫作全等形。能够完全重合的两个三角形叫作全等三角形。全等符号是“$\cong$”。
2. 全等三角形的性质:全等三角形的对应边相等,对应角也相等。
二、三角形全等的判定方法
1.一般三角形全等的条件:
2.直角三角形全等的条件:
3.三角形不一定全等的条件:
4.尺规作图:利用三角形全等的判定条件
1.一般三角形全等的条件:
SSS
、SAS
、ASA
、AAS
.2.直角三角形全等的条件:
SSS
、SAS
、ASA
、AAS
、HL
.3.三角形不一定全等的条件:
SSA
.4.尺规作图:利用三角形全等的判定条件
SAS
作一个角等于已知角.
答案:
【解析】:
本题主要考察三角形全等的判定方法以及尺规作图的知识点。
1. 对于一般三角形,全等的判定条件主要有四种,分别是边边边(SSS)、边角边(SAS)、角边角(ASA)、角角边(AAS)。
2. 对于直角三角形,由于存在一个直角,所以全等的判定条件除了上述四种外,还有一种特殊的情况,即斜边和一条直角边对应相等(HL)。
3. 三角形不一定全等的条件,通常指的是只有两边和其中一边的对角对应相等(SSA),这种情况不能判定两个三角形全等。
4. 尺规作图部分,我们可以利用三角形全等的判定条件边角边(SAS)来作一个角等于已知角。
【答案】:
1. 一般三角形全等的条件:$SSS$、$SAS$、$ASA$、$AAS$。
2. 直角三角形全等的条件:$SSS$、$SAS$、$ASA$、$AAS$、$HL$。
3. 三角形不一定全等的条件:$SSA$。
4. 尺规作图:利用三角形全等的判定条件$SAS$作一个角等于已知角。
本题主要考察三角形全等的判定方法以及尺规作图的知识点。
1. 对于一般三角形,全等的判定条件主要有四种,分别是边边边(SSS)、边角边(SAS)、角边角(ASA)、角角边(AAS)。
2. 对于直角三角形,由于存在一个直角,所以全等的判定条件除了上述四种外,还有一种特殊的情况,即斜边和一条直角边对应相等(HL)。
3. 三角形不一定全等的条件,通常指的是只有两边和其中一边的对角对应相等(SSA),这种情况不能判定两个三角形全等。
4. 尺规作图部分,我们可以利用三角形全等的判定条件边角边(SAS)来作一个角等于已知角。
【答案】:
1. 一般三角形全等的条件:$SSS$、$SAS$、$ASA$、$AAS$。
2. 直角三角形全等的条件:$SSS$、$SAS$、$ASA$、$AAS$、$HL$。
3. 三角形不一定全等的条件:$SSA$。
4. 尺规作图:利用三角形全等的判定条件$SAS$作一个角等于已知角。
三、角的平分线的性质与判定
1.角平分线的性质.
(1)
(2)由角平分线的定义知:角平分线把一个角分成两个相等的角.
2.角平分线的判定.
(1)
(2)由角平分线的定义知:把一个角分成两个相等的角的射线一定是这个角的平分线.
3.利用尺规作一个已知角的平分线,其原理是
1.角平分线的性质.
(1)
角的平分线上的点到角的两边的距离相等
;(2)由角平分线的定义知:角平分线把一个角分成两个相等的角.
2.角平分线的判定.
(1)
角的内部到角的两边的距离相等的点在角的平分线上
;(2)由角平分线的定义知:把一个角分成两个相等的角的射线一定是这个角的平分线.
3.利用尺规作一个已知角的平分线,其原理是
SSS
.
答案:
1.
(1)角的平分线上的点到角的两边的距离相等
2.
(1)角的内部到角的两边的距离相等的点在角的平分线上
3.SSS
(1)角的平分线上的点到角的两边的距离相等
2.
(1)角的内部到角的两边的距离相等的点在角的平分线上
3.SSS
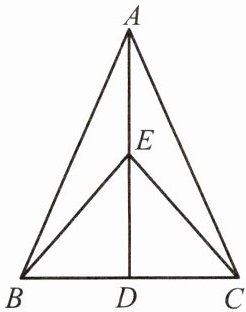
例1 如图,在△ABC中,AB= AC,D是BC的中点,点E在AD上.求证:
(1)△ABD≌△ACD;(2)BE= CE.
(1)△ABD≌△ACD;(2)BE= CE.

答案:
(1)证明:
∵D是BC的中点,
∴BD=CD,
在△ABD和△ACD中,
AB=AC,
AD=AD,
BD=CD,
∴△ABD≌△ACD(SSS)。
(2)证明:由
(1)知△ABD≌△ACD,
∴∠BAE=∠CAE,
在△ABE和△ACE中,
AB=AC,
∠BAE=∠CAE,
AE=AE,
∴△ABE≌△ACE(SAS),
∴BE=CE。
(1)证明:
∵D是BC的中点,
∴BD=CD,
在△ABD和△ACD中,
AB=AC,
AD=AD,
BD=CD,
∴△ABD≌△ACD(SSS)。
(2)证明:由
(1)知△ABD≌△ACD,
∴∠BAE=∠CAE,
在△ABE和△ACE中,
AB=AC,
∠BAE=∠CAE,
AE=AE,
∴△ABE≌△ACE(SAS),
∴BE=CE。
1.如图,在四边形ABCD中,∠BAC= ∠DAC,请补充一个条件:
AB=AD(或∠ACB=∠ACD或∠B=∠D)
,使△ABC≌△ADC.
答案:
解:AB=AD(或∠ACB=∠ACD或∠B=∠D)
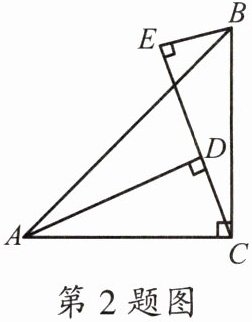
2.如图,∠ACB= 90°,AC= BC,AD⊥CE,BE⊥CE,垂足分别是D,E.若AD= 3,BE= 1,则DE的长是(
A.1
B.3/2
C.2
D.5/2
C
)
A.1
B.3/2
C.2
D.5/2
答案:
【解析】:本题可根据已知条件证明三角形全等,再利用全等三角形的性质求出$DE$的长。
步骤一:分析已知条件
已知$\angle ACB = 90^{\circ}$,$AD\perp CE$,$BE\perp CE$,所以$\angle ADC=\angle E = 90^{\circ}$。
因为$\angle ACB = 90^{\circ}$,所以$\angle ACD+\angle BCE = 90^{\circ}$,又因为$\angle ADC = 90^{\circ}$,在$\triangle ACD$中$\angle ACD+\angle CAD = 90^{\circ}$,根据同角的余角相等,可得$\angle CAD=\angle BCE$。
步骤二:证明三角形全等
在$\triangle ACD$和$\triangle CBE$中:
$\begin{cases}\angle ADC=\angle E\\\angle CAD=\angle BCE\\AC = BC\end{cases}$
根据全等三角形的判定定理$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle ACD\cong\triangle CBE$。
步骤三:利用全等三角形的性质求线段长度
由全等三角形的性质可知,全等三角形的对应边相等,因为$\triangle ACD\cong\triangle CBE$,所以$CD = BE$,$AD = CE$。
已知$AD = 3$,$BE = 1$,则$CE = 3$,$CD = 1$。
根据线段的和差关系,$DE = CE - CD$,将$CE = 3$,$CD = 1$代入可得$DE = 3 - 1 = 2$。
【答案】:C
步骤一:分析已知条件
已知$\angle ACB = 90^{\circ}$,$AD\perp CE$,$BE\perp CE$,所以$\angle ADC=\angle E = 90^{\circ}$。
因为$\angle ACB = 90^{\circ}$,所以$\angle ACD+\angle BCE = 90^{\circ}$,又因为$\angle ADC = 90^{\circ}$,在$\triangle ACD$中$\angle ACD+\angle CAD = 90^{\circ}$,根据同角的余角相等,可得$\angle CAD=\angle BCE$。
步骤二:证明三角形全等
在$\triangle ACD$和$\triangle CBE$中:
$\begin{cases}\angle ADC=\angle E\\\angle CAD=\angle BCE\\AC = BC\end{cases}$
根据全等三角形的判定定理$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle ACD\cong\triangle CBE$。
步骤三:利用全等三角形的性质求线段长度
由全等三角形的性质可知,全等三角形的对应边相等,因为$\triangle ACD\cong\triangle CBE$,所以$CD = BE$,$AD = CE$。
已知$AD = 3$,$BE = 1$,则$CE = 3$,$CD = 1$。
根据线段的和差关系,$DE = CE - CD$,将$CE = 3$,$CD = 1$代入可得$DE = 3 - 1 = 2$。
【答案】:C
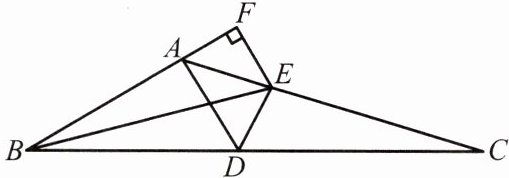
例2 如图,在△ABC中,点D在BC边上,∠BAD= 100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF= 50°,连接DE.
(1)求∠CAD的度数;
(2)求证:DE平分∠ADC;
(3)若AB= 7,AD= 4,CD= 8,且S△ACD= 15,求△ABE的面积.
分析:(1)根据直角三角形的性质求出∠FAE,根据补角的定义计算,得到答案.(2)过点E作EG⊥AD于点G,EH⊥BC于点H,根据角平分线的性质得到EF= EG,EF= EH,等量代换得到EG= EH,根据角平分线的判定定理证明结论.(3)根据三角形的面积公式求出EG,再根据三角形的面积公式计算,得到答案.
(1)求∠CAD的度数;
(2)求证:DE平分∠ADC;
(3)若AB= 7,AD= 4,CD= 8,且S△ACD= 15,求△ABE的面积.
分析:(1)根据直角三角形的性质求出∠FAE,根据补角的定义计算,得到答案.(2)过点E作EG⊥AD于点G,EH⊥BC于点H,根据角平分线的性质得到EF= EG,EF= EH,等量代换得到EG= EH,根据角平分线的判定定理证明结论.(3)根据三角形的面积公式求出EG,再根据三角形的面积公式计算,得到答案.

答案:
1. (1)
解:
在$Rt\triangle AEF$中,$\angle AFE = 90^{\circ}$,$\angle AEF = 50^{\circ}$。
根据直角三角形两锐角互余,可得$\angle FAE=90^{\circ}-\angle AEF = 90 - 50=40^{\circ}$。
又因为$\angle BAD = 100^{\circ}$,根据$\angle CAD=180^{\circ}-\angle BAD-\angle FAE$(平角为$180^{\circ}$)。
所以$\angle CAD = 180^{\circ}-100^{\circ}-40^{\circ}=40^{\circ}$。
2. (2)
证明:
过点$E$作$EG\perp AD$于点$G$,$EH\perp BC$于点$H$。
因为$BE$平分$\angle ABC$,$EF\perp AB$,$EH\perp BC$,根据角平分线的性质:角平分线上的点到角两边的距离相等,所以$EF = EH$。
又因为$\angle FAE=\angle CAD = 40^{\circ}$,$EF\perp AB$,$EG\perp AD$,根据角平分线的性质:角平分线上的点到角两边的距离相等,所以$EF = EG$。
则$EG = EH$。
因为$EG\perp AD$,$EH\perp BC$,根据角平分线的判定:到角两边距离相等的点在角的平分线上,所以$DE$平分$\angle ADC$。
3. (3)
解:
因为$\angle CAD = 40^{\circ}$,$EF\perp AB$,$EG\perp AD$,所以$EF = EG$。
已知$S_{\triangle ACD}=\frac{1}{2}AD\cdot EG+\frac{1}{2}CD\cdot EH$,又$EG = EH$,$AD = 4$,$CD = 8$,$S_{\triangle ACD}=15$。
则$S_{\triangle ACD}=\frac{1}{2}(AD + CD)\cdot EG$,即$15=\frac{1}{2}(4 + 8)\cdot EG$。
化简可得$15 = 6EG$,解得$EG=\frac{5}{2}$,所以$EF=\frac{5}{2}$。
因为$S_{\triangle ABE}=\frac{1}{2}AB\cdot EF$,$AB = 7$,$EF=\frac{5}{2}$。
所以$S_{\triangle ABE}=\frac{1}{2}×7×\frac{5}{2}=\frac{35}{4}$。
综上,(1)$\angle CAD$的度数为$40^{\circ}$;(2)证明过程如上述;(3)$\triangle ABE$的面积为$\frac{35}{4}$。
解:
在$Rt\triangle AEF$中,$\angle AFE = 90^{\circ}$,$\angle AEF = 50^{\circ}$。
根据直角三角形两锐角互余,可得$\angle FAE=90^{\circ}-\angle AEF = 90 - 50=40^{\circ}$。
又因为$\angle BAD = 100^{\circ}$,根据$\angle CAD=180^{\circ}-\angle BAD-\angle FAE$(平角为$180^{\circ}$)。
所以$\angle CAD = 180^{\circ}-100^{\circ}-40^{\circ}=40^{\circ}$。
2. (2)
证明:
过点$E$作$EG\perp AD$于点$G$,$EH\perp BC$于点$H$。
因为$BE$平分$\angle ABC$,$EF\perp AB$,$EH\perp BC$,根据角平分线的性质:角平分线上的点到角两边的距离相等,所以$EF = EH$。
又因为$\angle FAE=\angle CAD = 40^{\circ}$,$EF\perp AB$,$EG\perp AD$,根据角平分线的性质:角平分线上的点到角两边的距离相等,所以$EF = EG$。
则$EG = EH$。
因为$EG\perp AD$,$EH\perp BC$,根据角平分线的判定:到角两边距离相等的点在角的平分线上,所以$DE$平分$\angle ADC$。
3. (3)
解:
因为$\angle CAD = 40^{\circ}$,$EF\perp AB$,$EG\perp AD$,所以$EF = EG$。
已知$S_{\triangle ACD}=\frac{1}{2}AD\cdot EG+\frac{1}{2}CD\cdot EH$,又$EG = EH$,$AD = 4$,$CD = 8$,$S_{\triangle ACD}=15$。
则$S_{\triangle ACD}=\frac{1}{2}(AD + CD)\cdot EG$,即$15=\frac{1}{2}(4 + 8)\cdot EG$。
化简可得$15 = 6EG$,解得$EG=\frac{5}{2}$,所以$EF=\frac{5}{2}$。
因为$S_{\triangle ABE}=\frac{1}{2}AB\cdot EF$,$AB = 7$,$EF=\frac{5}{2}$。
所以$S_{\triangle ABE}=\frac{1}{2}×7×\frac{5}{2}=\frac{35}{4}$。
综上,(1)$\angle CAD$的度数为$40^{\circ}$;(2)证明过程如上述;(3)$\triangle ABE$的面积为$\frac{35}{4}$。
查看更多完整答案,请扫码查看


