《2025年巅峰对决八年级数学上册人教版》

1.等边三角形的定义:三边都相等的三角形是等边三角形.

答案： 【解析】：
本题考查等边三角形的定义。等边三角形是三角形的一种，其特点是三边的长度都相等。根据这个定义，我们可以填写题目中的空白部分。
【答案】：
相等

2.等边三角形的性质.
(1)等边三角形的三边都相等;
(2)等边三角形的三个角都相等,并且每一个角都等于60°.
符号语言:
∵△ABC 是等边三角形,
∴AB= BC= AC,∠A= ∠B= ∠C= 60°.

答案： 【解析】：
题目考查等边三角形的性质，特别是其角度的性质。等边三角形的三个角都是相等的，并且由于三角形的内角和为$180^\circ$，所以每个角都是$60^\circ$。
【答案】：
(2)相等；$60{^\circ}$。

3.等边三角形的判定.
(1)三边都相等的三角形是等边三角形.
符号语言:
∵AB= BC= AC,
∴△ABC 是等边三角形.
(2)三个角都相等的三角形是等边三角形.
符号语言:
∵∠A= ∠B= ∠C,
∴△ABC 是等边三角形.
(3)有一个角是60°的等腰三角形是等边三角形.
符号语言:
∵∠A(或∠B 或∠C)= 60°,AB= AC,
∴△ABC 是等边三角形.

答案： 【解析】：
本题考查等边三角形的判定条件。等边三角形是三条边都相等或三个角都相等的三角形，或者有一个角是60°的等腰三角形也是等边三角形。
(1) 根据等边三角形的定义，三边都相等的三角形是等边三角形。
(2) 同样，根据等边三角形的性质，三个内角都相等的三角形，且每个内角为60°，也是等边三角形。
(3) 对于等腰三角形，如果其中一个角为60°，则该等腰三角形必定是等边三角形，因为等腰三角形的两个底角相等，若其中一个角为60°，则其他两个角也必定为60°，从而形成等边三角形。
【答案】：
(1) 三边
(2) 三个角
(3) $60°$

例1 如图,△ABC 是等边三角形,DE//BC,分别交AC,AB 于点 D,E.求证:△ADE 是等边三角形.
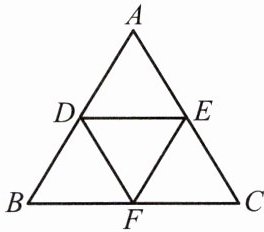
分析:由于 DE//BC,则∠AED= ∠B,∠ADE= ∠C,易得△ADE 的三个角相等,从而得证.

思考:
(1)若将条件 DE//BC 改为 AD= AE,△ADE 是等边三角形吗?试说明理由.
(2)如图,若 D,E,F 分别是等边△ABC 三边的中点,则△DEF 是等边三角形吗?为什么?

答案： 证明：
∵△ABC是等边三角形，
∴∠A=∠B=∠C=60°。
∵DE//BC，
∴∠AED=∠B=60°，∠ADE=∠C=60°。
∴∠A=∠ADE=∠AED=60°。
∴△ADE是等边三角形。
思考：
(1)是等边三角形。理由：
∵△ABC是等边三角形，
∴∠A=60°。
∵AD=AE，
∴△ADE是等腰三角形。
∵∠A=60°，
∴△ADE是等边三角形。
(2)是等边三角形。理由：
∵△ABC是等边三角形，
∴AB=BC=AC。
∵D,E,F分别是等边△ABC三边的中点，
∴DE、EF、FD是△ABC的中位线。
∴DE=1/2BC，EF=1/2AC，FD=1/2AB。
∵AB=BC=AC，
∴DE=EF=FD。
∴△DEF是等边三角形。

1.如图,E 是等边△ABC 中 AC 边上的点,∠1= ∠2,BE= CD,则△ADE 的形状是(A)

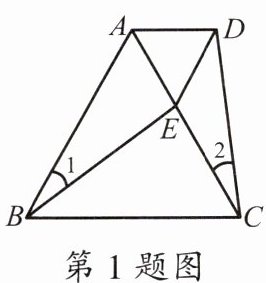
A.等边三角形
B.直角三角形
C.不等边三角形
D.不能确定

答案： 【解析】：本题可先根据等边三角形的性质得出相关边和角的关系，再通过全等三角形的判定定理证明$\triangle ABE$和$\triangle ACD$全等，进而得到$AE = AD$，最后结合$\angle 1 = \angle 2$求出$\angle EAD$的度数，从而判断$\triangle ADE$的形状。
步骤一：分析等边三角形$\triangle ABC$的性质
已知$\triangle ABC$是等边三角形，根据等边三角形的性质可知：$AB = AC$，$\angle BAC = 60^{\circ}$。
步骤二：证明$\triangle ABE\cong\triangle ACD$
在$\triangle ABE$和$\triangle ACD$中，
$\begin{cases}AB = AC\\\angle 1 = \angle 2\\BE = CD\end{cases}$
根据全等三角形的判定定理（SAS：两边及其夹角对应相等的三角形全等），可得$\triangle ABE\cong\triangle ACD$。
步骤三：根据全等三角形的性质得到$AE = AD$，$\angle BAE = \angle CAD$
因为$\triangle ABE\cong\triangle ACD$，根据全等三角形的性质（全等三角形的对应边相等，对应角相等），所以$AE = AD$，$\angle BAE = \angle CAD$。
步骤四：求出$\angle EAD$的度数
因为$\angle BAC = \angle BAE + \angle EAC = 60^{\circ}$，且$\angle BAE = \angle CAD$，所以$\angle EAD = \angle CAD + \angle EAC = \angle BAE + \angle EAC = 60^{\circ}$。
步骤五：判断$\triangle ADE$的形状
由$AE = AD$，$\angle EAD = 60^{\circ}$，根据有一个角是$60^{\circ}$的等腰三角形是等边三角形，可知$\triangle ADE$是等边三角形。
【答案】：A

2.如图,D,E,F 分别是等边△ABC 各边上的点,且AD= BE= CF,则△DEF 的形状是(A)
A.等边三角形
B.腰和底边不相等的等腰三角形
C.直角三角形
D.不等边三角形

答案： 证明：
∵△ABC是等边三角形，
∴AB=BC=AC，∠A=∠B=∠C=60°．
∵AD=BE=CF，
∴AB-AD=BC-BE=AC-CF，即BD=CE=AF．
在△ADF和△BED中，
AD=BE，∠A=∠B，AF=BD，
∴△ADF≌△BED（SAS），
∴DF=ED．
同理可证△BED≌△CFE（SAS），
∴ED=FE．
∴DF=ED=FE，
∴△DEF是等边三角形．
答案：A

例2 如图,在等边△ABC 中,点 E,F 分别以相同的速度从点 A,B 出发,点 E 沿 AB 方向运动,点 F 沿 BC 方向运动.
(1)如图1,当点 E,F 分别在线段 AB,BC 上时,连接 CE,AF 相交于点 P,试求∠CPF 的度数.
(2)如图2,当点 E,F 分别运动到 AB,BC 的延长线上时,EC 的延长线交 AF 于点 P,(1)中∠CPF 的度数发生变化了吗?若没发生变化,请说明理由;若发生变化,请求出其度数.
分析:(1)由已知容易得到△AEC≌△BFA,则∠ACE= ∠BAF,从而利用三角形外角定理得到∠CPF= ∠FAC+∠ACE= ∠FAC+∠BAF= ∠BAC;
(2)显然∠CPF 的度数发生了变化,仍然证明△AEC≌△BFA,得∠E= ∠F,从而易得∠CPF= ∠CBE= 120°.

答案：
(1)解：
∵△ABC是等边三角形，
∴AB=AC=BC，∠BAC=∠ABC=∠ACB=60°。
∵点E，F分别以相同的速度从点A，B出发，
∴AE=BF。
在△AEC和△BFA中，
$\left\{\begin{array}{l}AE=BF\\ \angle EAC=\angle FBA=60°\\ AC=BA\end{array}\right.$
∴△AEC≌△BFA(SAS)。
∴∠ACE=∠BAF。
∵∠CPF是△APC的外角，
∴∠CPF=∠FAC+∠ACE=∠FAC+∠BAF=∠BAC=60°。
(2)解：∠CPF的度数发生变化，∠CPF=120°。
理由：
∵△ABC是等边三角形，
∴AB=AC=BC，∠BAC=∠ABC=∠ACB=60°。
∵点E，F分别以相同的速度从点A，B出发运动到延长线上，
∴AE=BF。
∵∠EAC=180°-∠BAC=120°，∠FBA=180°-∠ABC=120°，
∴∠EAC=∠FBA。
在△AEC和△BFA中，
$\left\{\begin{array}{l}AE=BF\\ \angle EAC=\angle FBA\\ AC=BA\end{array}\right.$
∴△AEC≌△BFA(SAS)。
∴∠E=∠F。
∵∠E+∠BCE=∠ABC=60°，∠BCE=∠PCF，
∴∠F+∠PCF=60°。
∴∠CPF=180°-(∠F+∠PCF)=180°-60°=120°。