《2025年巅峰对决八年级数学上册人教版》

1. 如图,在四边形$ABCD$中,$AC垂直平分BD$,垂足为$E$,下列结论中不一定成立的是(C)
A.$AB= AD$
B.$CA平分\angle BCD$
C.$AB= BD$
D.$\triangle BEC\cong\triangle DEC$

答案： 【解析】：本题可根据线段垂直平分线的性质以及全等三角形的判定定理来逐一分析选项。
选项A：判断$AB = AD$是否成立
已知$AC$垂直平分$BD$，根据线段垂直平分线的性质：线段垂直平分线上的点到这条线段的两个端点的距离相等。
因为点$A$在$BD$的垂直平分线$AC$上，所以$AB = AD$，该选项一定成立。
选项B：判断$CA$平分$\angle BCD$是否成立
因为$AC$垂直平分$BD$，所以$CE$是$BD$的垂直平分线，那么$BE = DE$，$\angle BEC=\angle DEC = 90^{\circ}$，且$AC$为公共边。
在$\triangle BEC$和$\triangle DEC$中，$\begin{cases}BE = DE\\\angle BEC=\angle DEC\\EC = EC\end{cases}$，根据“边角边”（$SAS$）判定定理可得$\triangle BEC\cong\triangle DEC$。
根据全等三角形的性质：全等三角形的对应角相等，所以$\angle BCE=\angle DCE$，即$CA$平分$\angle BCD$，该选项一定成立。
选项C：判断$AB = BD$是否成立
由已知条件$AC$垂直平分$BD$，只能推出点$A$到$B$、$D$两点的距离相等，即$AB = AD$，以及$\triangle BEC\cong\triangle DEC$等结论，但无法得出$AB = BD$，该选项不一定成立。
选项D：判断$\triangle BEC\cong\triangle DEC$是否成立
前面在分析选项B时已经证明，因为$BE = DE$，$\angle BEC=\angle DEC = 90^{\circ}$，$EC = EC$，根据“边角边”（$SAS$）判定定理可得$\triangle BEC\cong\triangle DEC$，该选项一定成立。
【答案】：C

2. 如图,在$\triangle ABC$中,$AB的垂直平分线交AB于点D$,交$BC于点E$.若$BC= 6$,$AC= 5$,则$\triangle ACE$的周长为(B)

A.8
B.11
C.16
D.17

答案： 解：
∵DE是AB的垂直平分线，
∴AE=BE。
∵BC=6，
∴BE+EC=BC=6，
∴AE+EC=6。
∵AC=5，
∴△ACE的周长=AC+AE+EC=5+6=11。
答案：B

3. 如图,在$\triangle ABC$中,$BC= 8$,$AB的垂直平分线交BC于点D$,$AC的垂直平分线交BC于点E$,则$\triangle ADE$的周长为 _____.

8

答案： 【解析】：本题可根据线段垂直平分线的性质，得到线段之间的等量关系，进而求出$\triangle ADE$的周长。
线段垂直平分线的性质为：线段垂直平分线上的点到这条线段的两个端点的距离相等。
已知$AB$的垂直平分线交$BC$于点$D$，根据上述性质可得$AD = BD$；
$AC$的垂直平分线交$BC$于点$E$，同理可得$AE = CE$。
$\triangle ADE$的周长为$AD + DE + AE$，将$AD = BD$，$AE = CE$代入可得：
$AD + DE + AE=BD + DE + CE$，而$BD + DE + CE = BC$。
已知$BC = 8$，所以$\triangle ADE$的周长为$8$。
【答案】：$8$

例2 如图,在$\triangle ABC$中,$EF是AB$的垂直平分线,$MN是BC$的垂直平分线,$EF与MN相交于点O$.求证:点$O必在AC$的垂直平分线上.
分析:因为到线段两端距离相等的点在线段的垂直平分线上,所以要判断点$O是否在AC$的垂直平分线上,只需判断$OA是否等于OC$即可.

归纳:
三角形的三边的垂直平分线交于一点.

答案： 【解析】：本题可根据线段垂直平分线的性质定理，分别证明$OA = OB$，$OB = OC$，进而得到$OA = OC$，再根据线段垂直平分线的判定定理证明点$O$在$AC$的垂直平分线上。
证明：
∵$EF$是$AB$的垂直平分线，$O$在$EF$上（已知），
根据线段垂直平分线上的点到这条线段的两个端点的距离相等，
∴$OA = OB$。
∵$MN$是$BC$的垂直平分线，$O$在$MN$上（已知），
同理可得$OB = OC$。
由$OA = OB$，$OB = OC$，可得$OA = OC$。
根据到一条线段的两个端点的距离相等的点，在这条线段的垂直平分线上，
∴点$O$必在$AC$的垂直平分线上。
【答案】：
证明：
∵$EF$是$AB$的垂直平分线，$O$在$EF$上，
∴$OA = OB$。
∵$MN$是$BC$的垂直平分线，$O$在$MN$上，
∴$OB = OC$。
∴$OA = OC$。
∴点$O$必在$AC$的垂直平分线上。

4. 元旦联欢会上,同学们玩抢凳子游戏,在与$A,B,C$三名同学距离相等的位置放一张凳子,谁先抢到凳子谁获胜.如果将$A,B,C三名同学所在位置看作\triangle ABC$的三个顶点,那么凳子应该放在$\triangle ABC$的(D)
A.三边中线的交点
B.三条角平分线的交点
C.三边上高的交点
D.三边垂直平分线的交点

答案： 【解析】：
本题主要考察线段垂直平分线的性质。
根据题目描述，凳子需要放在与$A,B,C$三名同学距离相等的位置，即需要找到一个点到三角形三个顶点的距离相等。
根据线段垂直平分线的性质，线段垂直平分线上的点到线段两个端点的距离相等。
因此，在三角形中，到三个顶点距离相等的点应当是三角形三边垂直平分线的交点。
A选项：三边中线的交点称为三角形的质心，质心到三边的距离之比为$2:1$，不符合题目要求。
B选项：三条角平分线的交点称为三角形的内心，内心到三角形三边的距离相等，但到三个顶点的距离不一定相等，不符合题目要求。
C选项：三边上高的交点称为三角形的垂心，垂心主要与三角形的高有关，不符合题目要求。
D选项：三边垂直平分线的交点，符合题目要求，到三角形三个顶点的距离相等。
综上所述，凳子应该放在三角形三边垂直平分线的交点上。
【答案】：
D

5. 如图,$AC= AD$,$BC= BD$,则有(A)

A.$AB垂直平分CD$
B.$CD垂直平分AB$
C.$AB与CD$互相垂直平分
D.$CD平分\angle ACB$

答案： 证明：
∵AC=AD，
∴点A在CD的垂直平分线上（到线段两端距离相等的点在这条线段的垂直平分线上）。
∵BC=BD，
∴点B在CD的垂直平分线上。
∵两点确定一条直线，
∴AB是CD的垂直平分线，即AB垂直平分CD。
答案：A

例3 如图,$AD平分\angle BAC$,$EF垂直平分AD$,交$BC延长线于点F$,连接$AF$.求证:$\angle B= \angle CAF$.
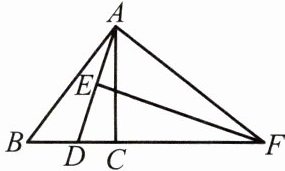
分析:$\angle B与\angle CAF$不在同一个三角形中,又因为$\angle B,\angle CAF$所在的三角形不全等,故欲证$\angle B= \angle CAF$,不能利用等腰三角形及全等三角形的性质.注意到$EF垂直平分AD$,所以可得$FA= FD$,因此$\angle FAD= \angle ADF$.又因为$\angle CAF= \angle FAD-\angle CAD$,$\angle B= \angle ADF-\angle BAD$,而$\angle CAD= \angle BAD$,至此,$\angle B= \angle CAF$得证.
]

答案： 【解析】：本题可根据线段垂直平分线的性质、角平分线的定义以及三角形外角的性质来证明$\angle B = \angle CAF$。
步骤一：根据线段垂直平分线的性质得到$FA = FD$，进而推出$\angle FAD=\angle ADF$。
已知$EF$垂直平分$AD$，根据线段垂直平分线的性质：线段垂直平分线上的点到这条线段的两个端点的距离相等，可得$FA = FD$。
再根据等腰三角形的性质：等腰三角形的两个底角相等，因为$FA = FD$，所以$\triangle FAD$是等腰三角形，那么$\angle FAD=\angle ADF$。
步骤二：根据角平分线的定义得到$\angle CAD=\angle BAD$。
已知$AD$平分$\angle BAC$，根据角平分线的定义：从一个角的顶点出发，把这个角分成相等的两个角的射线叫做这个角的平分线，可得$\angle CAD=\angle BAD$。
步骤三：根据三角形外角的性质表示出$\angle CAF$和$\angle B$。
根据三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角之和。
在$\triangle ADF$中，$\angle FAD$是外角，$\angle CAF=\angle FAD - \angle CAD$；
在$\triangle ABD$中，$\angle ADF$是外角，$\angle B=\angle ADF - \angle BAD$。
步骤四：结合前面的结论证明$\angle B = \angle CAF$。
因为$\angle FAD=\angle ADF$，$\angle CAD=\angle BAD$，所以$\angle CAF=\angle FAD - \angle CAD=\angle ADF - \angle BAD=\angle B$，即$\angle B = \angle CAF$。
【答案】：证明：
∵$EF$垂直平分$AD$，
∴$FA = FD$（线段垂直平分线上的点到这条线段的两个端点的距离相等），
∴$\angle FAD=\angle ADF$（等边对等角）。
∵$AD$平分$\angle BAC$，
∴$\angle CAD=\angle BAD$（角平分线的定义）。
∵$\angle CAF=\angle FAD - \angle CAD$，$\angle B=\angle ADF - \angle BAD$，
∴$\angle B = \angle CAF$。

6. 如图,在$\triangle ABC$中,$\angle A= 56^\circ$,$PD垂直平分AB$,$PE垂直平分BC$,则$\angle BPC$的度数为(B)
A.$124^\circ$
B.$112^\circ$
C.$108^\circ$
D.$118^\circ$

答案： 【解析】：本题可根据线段垂直平分线的性质得到相等的线段，进而得到相等的角，再结合三角形内角和定理求出$\angle BPC$的度数。
步骤一：根据线段垂直平分线的性质得到相等的角
已知$PD$垂直平分$AB$，根据线段垂直平分线的性质：线段垂直平分线上的点到这条线段的两个端点的距离相等，可得$PA = PB$。
因为等边对等角，所以$\angle ABP = \angle A = 56^{\circ}$。
同理，因为$PE$垂直平分$BC$，所以$PB = PC$，则$\angle PBC = \angle PCB$。
步骤二：求出$\angle ABC + \angle ACB$的度数
在$\triangle ABC$中，根据三角形内角和定理：三角形内角和为$180^{\circ}$，已知$\angle A = 56^{\circ}$，则$\angle ABC + \angle ACB = 180^{\circ} - \angle A = 180^{\circ} - 56^{\circ} = 124^{\circ}$。
步骤三：求出$\angle PBC + \angle PCB$的度数
因为$\angle ABP = \angle A = 56^{\circ}$，所以$\angle PBC + \angle PCB = \angle ABC + \angle ACB - (\angle ABP + \angle ACP)$，又因为$\angle ABP = \angle A$，$\angle ACP = \angle ABP$（由$PA = PB = PC$可得），所以$\angle PBC + \angle PCB = \angle ABC + \angle ACB - 2\angle ABP = 124^{\circ} - 56^{\circ} = 68^{\circ}$。
步骤四：求出$\angle BPC$的度数
在$\triangle BPC$中，根据三角形内角和定理，$\angle BPC = 180^{\circ} - (\angle PBC + \angle PCB) = 180^{\circ} - 68^{\circ} = 112^{\circ}$。
【答案】：B