《2025年巅峰对决八年级数学上册人教版》

5.一张正方形纸片经过两次对折,并在如图所示的位置上剪去一个小正方形,打开后是 (C)

答案： 【解析】：本题可根据正方形的对称性以及折叠的性质，通过分析剪去小正方形后展开的过程来确定打开后的图形。
步骤一：分析正方形的对称性和折叠性质
正方形是中心对称图形，沿对角线对折后，折痕是正方形的对称轴，对折后的两部分能够完全重合。
步骤二：分析第一次对折后的情况
将正方形纸片第一次对折后，得到一个等腰直角三角形，此时在如图所示位置剪去一个小正方形，那么在展开第一次对折时，由于对称性，会在与剪去小正方形相对称的位置也出现一个小正方形。
步骤三：分析第二次对折后的情况
再进行第二次对折，同样由于正方形的对称性，在展开第二次对折时，会在相应的对称位置也出现小正方形。
步骤四：确定打开后的图形
综合两次对折和剪去小正方形的过程，打开后会在正方形的四个角落各出现一个小正方形，且这四个小正方形关于正方形的中心对称，所以打开后是选项C的图形。
【答案】：C

1.如图,由一个平面图形可以得到与它关于一条直线对称的另一个图形,这个图形与原图形的形状、大小完全相同.
注意：
(1)新图形上的每一点都是原图形上的某一点关于这条直线的对称点；
(2)连接任意一对对应点的线段被对称轴垂直平分.
2.成轴对称图形的作法.
(1)先找出确定图形的关键点,然后作出每个关键点关于这条直线的对称点(注意对称点的连线段与对称轴垂直,并且对称点到对称轴等距)；
(2)然后连接各对称点即得到关于这条直线对称的图形.

答案： 【解析】：本题考查轴对称图形的性质。如果一个平面图形沿着一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线叫做对称轴。轴对称图形具有以下性质：
成轴对称的两个图形全等；
如果两个图形成轴对称，那么对称轴是对称点连线的垂直平分线。
因此，新图形与原图形在形状和大小上是完全相同的。
【答案】：形状；大小

例1 已知：△ABC 和过点 A 的直线 MN 如图所示.
求作：△A'B'C',使△A'B'C'与△ABC 关于直线 MN 对称.
归纳：
几何图形都可以看成由点组成的.对于某些图形,只要画出图形中的一些特殊点(如线段端点、圆的圆心等)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.

答案： 解：作法：
1. 过点 B 作直线 MN 的垂线，垂足为点 O，延长 BO 至 B'，使 OB' = OB，则点 B' 为点 B 关于直线 MN 的对称点；
2. 同理，作出点 C 关于直线 MN 的对称点 C'；
3. 因为点 A 在直线 MN 上，所以点 A 的对称点 A' 与点 A 重合；
4. 连接 A'B'、B'C'、C'A'，则△A'B'C'即为所求作的三角形。

1.如图,△ABC 和△A'B'C'关于直线 MN 对称,P 是直线 MN 上一点,连接 PA,PA',AA',下列结论不一定正确的是(B)
A.∠B= ∠B'
B.BC= PA
C.PA= PA'
D.直线 MN 是线段 AA'的垂直平分线

答案： 【解析】：本题可根据轴对称的性质，逐一分析每个选项。
选项A：
如果两个图形关于某条直线对称，那么这两个图形全等，全等图形的对应角相等。
因为$\triangle ABC$和$\triangle A'B'C'$关于直线$MN$对称，所以$\triangle ABC\cong\triangle A'B'C'$，$\angle B$与$\angle B'$是对应角，所以$\angle B = \angle B'$，该选项正确。
选项B：
由轴对称的性质可知，对应线段相等，即$BC = B'C'$，$AA'$被直线$MN$垂直平分，$PA = PA'$ ，但$BC$与$PA$并没有直接的等量关系，该选项不一定正确。
选项C：
根据轴对称的性质：如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。
因为$\triangle ABC$和$\triangle A'B'C'$关于直线$MN$对称，$P$是直线$MN$上一点，$A$与$A'$是对应点，所以直线$MN$是线段$AA'$的垂直平分线，即$PA = PA'$，该选项正确。
选项D：
由于$\triangle ABC$和$\triangle A'B'C'$关于直线$MN$对称，$A$与$A'$是对应点，根据轴对称的性质可知，直线$MN$是线段$AA'$的垂直平分线，该选项正确。
【答案】：B

2.把一张长方形的纸片按如图所示的方式折叠后,点 B,D 分别落在点 B',D'处.若∠AOB'= 50°,则∠B'OG 的度数为(B)
A.55°
B.65°
C.75°
D.80°

答案： 解：由折叠性质得∠BOG=∠B'OG。
∵∠AOB'+∠BOG+∠B'OG=180°，∠AOB'=50°，
∴50°+2∠B'OG=180°，
解得∠B'OG=65°。
答案：B

例2 如图甲,正方形被划分成16个全等的三角形,将其中若干个三角形涂黑,且满足下列条件：
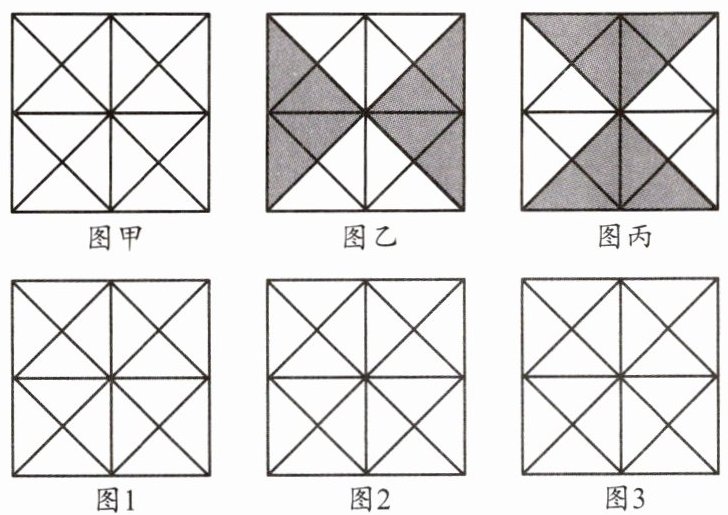
(1)涂黑部分的面积是原正方形面积的一半；
(2)涂黑部分成轴对称图形.
图乙所示是一种涂法,请在图1~3中分别设计另外三种涂法.(在所设计的图案中,若涂黑部分全等,则认为是同一种涂法,如图乙与图丙)

答案： 【解析】：本题主要考查利用轴对称设计图案，关键是掌握轴对称图形的性质。
(1)根据轴对称图形的性质，涂黑4个三角形，它们可以组成一个与正方形的对角线对称的图形，这样涂黑部分的面积就是原正方形面积的一半，且涂黑部分成轴对称图形。
(2)同样，涂黑8个三角形，使它们关于正方形的两条对边中点连线对称，也能满足题目要求。
(3)另外，还可以涂黑8个三角形，使它们关于正方形的两条对角线对称，这样也能满足题目条件。
【答案】：图略（按照上述分析，在图1、图2、图3中分别设计出满足条件的涂法）。