《2025年春如金卷课时作业AB本八年级数学上册北师大版》

4. 以下列各组数据为三角形三边长,能构成直角三角形的是(D)
A. 4 cm,8 cm,7 cm
B. 3 cm,5 cm,2 cm
C. 2 cm,2 cm,4 cm
D. 13 cm,12 cm,5 cm

答案： D

5. 如图,在$△ABC$中,$D是边BC$上一点,若$AB= 10,BD= 6,AD= 8,AC= 17$。
(1)求$∠ADB$的度数。90°
(2)求$CD$的长。15

答案： 解:
(1)因为$AB = 10$，$BD = 6$，$AD = 8$，所以$BD^{2}+AD^{2}=6^{2}+8^{2}=100 = AB^{2}$，所以$\triangle ABD$是直角三角形，即$∠ADB = 90^{\circ }$；
(2)由
(1)得$∠ADB = ∠ADC = 90^{\circ }$，所以在Rt$\triangle ADC$中，由勾股定理得：$CD^{2}=AC^{2}-AD^{2}=17^{2}-8^{2}=15^{2}$，所以$CD = 15$。

6. 如图,在$7×7$的网格中,每个小正方形的边长都为1。
(1)求$△ABC$的面积;5
(2)$△ABC$是直角三角形吗? 请说明理由。是，因为$AC^{2}=2^{2}+1^{2}=5$，$BC^{2}=2^{2}+4^{2}=20$，$AB^{2}=4^{2}+3^{2}=25$，所以$AC^{2}+BC^{2}=AB^{2}$，所以$\triangle ABC$是直角三角形。

答案： 解:
(1)$S_{\triangle ABC}=4×4-\frac {1}{2}×4×2-\frac {1}{2}×3×4-\frac {1}{2}×1×2=16 - 4 - 6 - 1 = 5$。
(2)因为$AC^{2}=2^{2}+1^{2}=5$，$BC^{2}=2^{2}+4^{2}=20$，$AB^{2}=4^{2}+3^{2}=25$，所以$AC^{2}+BC^{2}=AB^{2}$，所以$\triangle ABC$是直角三角形。

7. 已知一个三角形的三边长分别为$3k,4k,5k$($k$为非零自然数),则这个三角形是直角三角形,理由是$(3k)^{2}+(4k)^{2}=(5k)^{2}$。

答案： 直角三角形 $(3k)^{2}+(4k)^{2}=(5k)^{2}$

8. 若一个三角形的三边长之比为$5:12:13$,且周长为$60cm$,则它的面积为120$cm^{2}$。

答案： 120

9. 若一个三角形的三边长分别为$25cm,15cm,20cm$,则这个三角形最长边上的高为12$cm$。

答案： 12

10. 【生活情境·测量距离】随着中国科技、经济的不断发展,5G信号的覆盖的广泛性和稳定性都有更好的表现。如图,有一辆汽车沿直线$AB$方向,由点$A向点B$行驶,已知点$C$为某个5G信号源,且点$C到点A和点B的距离分别为60m和80m$,且$AB= 100m$,信号源中心周围$50m$及以内可以接收到5G信号。
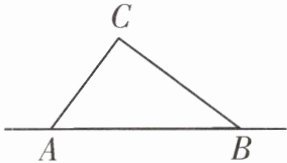
(1)汽车在从点$A向点B$行驶的过程中,能接收到5G信号吗? 为什么?
(2)若汽车的速度为$10m/s$,请问有多长时间可以接收到5G信号?

答案：
解:
(1)汽车在从点A向点B行驶的过程中，能接收到5G信号，理由如下:过点C作$CD⊥AB$于点D，如图1所示。
　　　　　　　　　　　　　
因为$AC = 60m$，$BC = 80m$，$AB = 100m$，$60^{2}+80^{2}=100^{2}$，所以$AC^{2}+BC^{2}=AB^{2}$，所以$∠ACB = 90^{\circ }$，所以$CD=\frac {\frac {1}{2}AC\cdot BC}{\frac {1}{2}AB}=\frac {\frac {1}{2}×60×80}{\frac {1}{2}×100}=48(m)$，因为$48m ＜ 50m$，所以汽车在从点A向点B行驶的过程中，能接收到5G信号；
(2)设点E，F在直线AB上，且$AE = AF = 50m$，如图2所示。
　　　　　　　　　　　　　
在Rt$\triangle CDE$中，$CD = 48m$，$CE = 50m$，$DE^{2}=CE^{2}-CD^{2}=50^{2}-48^{2}=14^{2}$，所以$DE = 14(m)$，同理：$DF = DE = 14m$，所以$EF = DE + DF = 14 + 14 = 28(m)$，所以$28÷10 = 2.8(s)$。
答:有2.8秒可以接收到5G信号。