第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
4. 点$A(-2,3)$关于x轴的对称点$A'$的坐标为 (
A. $(2,-3)$
B. $(-2,-3)$
C. $(-2,3)$
D. $(2,3)$
B
)A. $(2,-3)$
B. $(-2,-3)$
C. $(-2,3)$
D. $(2,3)$
答案:
B
5. 蝴蝶标本可以近似地看作轴对称图形。如图, 将一只蝴蝶标本放在平面直角坐标系中, 如果图中点$A的坐标为(5,3)$, 则其关于$y轴对称的点B$的坐标为 (
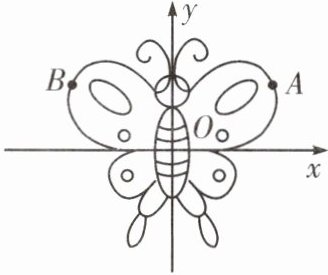
A. $(5,-3)$
B. $(-5,3)$
C. $(-5,-3)$
D. $(3,5)$
B
)
A. $(5,-3)$
B. $(-5,3)$
C. $(-5,-3)$
D. $(3,5)$
答案:
B
6. 已知点$P关于y轴的对称点P_{1}的坐标是(2,3)$, 那么点$P关于x轴的对称点P_{2}$的坐标为 (
A. $(-3,-2)$
B. $(-2,3)$
C. $(-2,-3)$
D. $(2,-3)$
C
)A. $(-3,-2)$
B. $(-2,3)$
C. $(-2,-3)$
D. $(2,-3)$
答案:
C
7. 已知图形$A在y$轴的右侧, 如果将图形$A上的所有点的横坐标都乘-1$, 纵坐标不变得到图形$B$, 则 (
A. 两个图形关于$x$轴对称
B. 两个图形关于$y$轴对称
C. 两个图形重合
D. 两个图形不关于任何一条直线对称
B
)A. 两个图形关于$x$轴对称
B. 两个图形关于$y$轴对称
C. 两个图形重合
D. 两个图形不关于任何一条直线对称
答案:
B
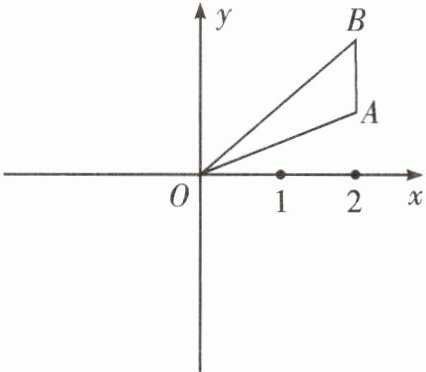
8. 如图, 点$A$,$B的坐标分别是(2,1)$,$(2,2)$。
(1) 作$\triangle ABO关于x$轴对称的图形, 并写出各顶点的坐标;
(2) 作$\triangle ABO关于y$轴对称的图形, 并写出各顶点的坐标。
(1) 作$\triangle ABO关于x$轴对称的图形, 并写出各顶点的坐标;
(2) 作$\triangle ABO关于y$轴对称的图形, 并写出各顶点的坐标。

答案:
解:
(1)作图,如图中△A1B1O,其各顶点的坐标是A1(2,−1),B1(2,−2),O(0,0)。
(2)作图,如图中△A2B2O,其各顶点的坐标是A2(−2,1),B2(−2,2),O(0,0)。

解:
(1)作图,如图中△A1B1O,其各顶点的坐标是A1(2,−1),B1(2,−2),O(0,0)。
(2)作图,如图中△A2B2O,其各顶点的坐标是A2(−2,1),B2(−2,2),O(0,0)。

9. 如图, 点$A在y$轴上,$\triangle AOB$是等腰三角形,$AB = OB$, 点$B关于y轴的对称点的坐标为(-5,3)$, 则点$A$的坐标为
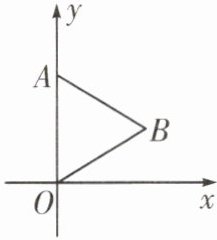
(0,6)
。
答案:
(0,6)
10. 如图, 在平面直角坐标系中, 已知点$A的坐标为(4,4)$, 若$\triangle ABC关于直线y = 1$成轴对称, 则点$B$的坐标为
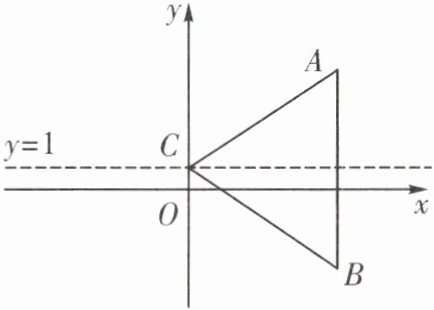
(4,−2)
。
答案:
(4,−2)
11. 如图, 在平面直角坐标系$xOy$中, 直线$l经过点M(3,0)$, 且平行于$y$轴, 给出如下定义: 点$P(x,y)先关于y轴对称得点P_{1}$, 再将点$P_{1}关于直线l对称得点P_{2}$, 则称点$P_{2}是点P关于y轴和直线l$的二次反射点。
(1) 已知$A(-4,0)$,$B(-2,0)$,$C(-3,1)$, 则它们关于$y轴和直线l的二次反射点A_{2}$,$B_{2}$,$C_{2}$的坐标分别是
(2) 若点$D的坐标是(a,0)$, 其中$a \lt 0$, 点$D关于y轴和直线l的二次反射点是点D_{2}$, 求线段$DD_{2}$的长。
(1) 已知$A(-4,0)$,$B(-2,0)$,$C(-3,1)$, 则它们关于$y轴和直线l的二次反射点A_{2}$,$B_{2}$,$C_{2}$的坐标分别是
(2,0),(4,0),(3,1)
;(2) 若点$D的坐标是(a,0)$, 其中$a \lt 0$, 点$D关于y轴和直线l的二次反射点是点D_{2}$, 求线段$DD_{2}$的长。
6
答案:
解:
(1)(2,0),(4,0),(3,1);
(2)点D关于y轴对称点的坐标为(−a,0),
所以(−a,0)关于直线l对称的点D2(6+a,0),
所以DD2=6+a−a=6。
(1)(2,0),(4,0),(3,1);
(2)点D关于y轴对称点的坐标为(−a,0),
所以(−a,0)关于直线l对称的点D2(6+a,0),
所以DD2=6+a−a=6。
查看更多完整答案,请扫码查看


