《2025年春如金卷课时作业AB本八年级数学上册北师大版》

9. 已知有23人在甲处劳动,17人在乙处劳动。现共调20人去支援,要使在甲处劳动的人数是在乙处劳动的人数的2倍。应调往甲、乙两处各多少人?

答案： 【解析】：设应调往甲处$x$人，则调往乙处$(20 - x)$人。调人后甲处有$(23 + x)$人，乙处有$(17+(20 - x))$人。根据在甲处劳动的人数是在乙处劳动的人数的$2$倍，可列方程$23 + x = 2\times(17+(20 - x))$，即$23 + x = 2\times(37 - x)$，展开括号得$23 + x = 74 - 2x$，移项得$x + 2x = 74 - 23$，合并同类项得$3x = 51$，解得$x = 17$。那么调往乙处的人数为$20 - 17 = 3$人。
【答案】：应调往甲处$17$人，调往乙处$3$人。

10. 如图,直线$l_{1}:y= 2x+1与直线l_{2}:y= -x+4相交于点P(1,b)$,直线$l_{1},l_{2}$与x轴分别交于A,B两点。
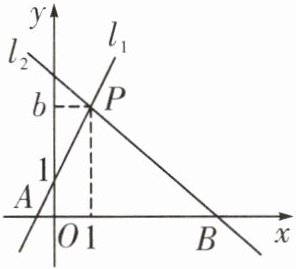
(1)求b的值3,并结合图象写出关于x,y的方程组$\left\{\begin{array}{l} 2x-y= -1,\\ -x-y= -4\end{array}\right. $的解$\begin{cases} x=1 \\ y=3 \end{cases}$;
(2)求$\triangle ABP$的面积$\frac{27}{4}$;
(3)垂直于x轴的直线$x= a与直线l_{1},l_{2}$分别交于点C,D,若线段CD的长为4,求出a的值$\frac{7}{3}$或$-\frac{1}{3}$。

答案： 【解析】：
### $(1)$求$b$的值以及方程组的解
- 求$b$的值：
已知点$P(1,b)$在直线$l_{1}:y = 2x + 1$上，将$x = 1$代入$y = 2x + 1$，可得$b=2\times1 + 1=3$。
- 求方程组的解：
方程组$\begin{cases}2x - y = - 1\\-x - y = - 4\end{cases}$可变形为$\begin{cases}y = 2x + 1\\y=-x + 4\end{cases}$。
因为直线$l_{1}:y = 2x + 1$与直线$l_{2}:y=-x + 4$相交于点$P(1,3)$，所以方程组$\begin{cases}2x - y = - 1\\-x - y = - 4\end{cases}$的解为$\begin{cases}x = 1\\y = 3\end{cases}$。
### $(2)$求$\triangle ABP$的面积
- 求$A$、$B$两点的坐标：
对于直线$l_{1}:y = 2x + 1$，令$y = 0$，则$2x+1 = 0$，解得$x=-\frac{1}{2}$，所以$A(-\frac{1}{2},0)$。
对于直线$l_{2}:y=-x + 4$，令$y = 0$，则$-x + 4 = 0$，解得$x = 4$，所以$B(4,0)$。
- 计算$AB$的长度：
根据两点间距离公式$AB=\vert x_{B}-x_{A}\vert$，可得$AB = 4-(-\frac{1}{2})=\frac{9}{2}$。
- 计算$\triangle ABP$的面积：
点$P$的纵坐标的绝对值$\vert y_{P}\vert$就是$\triangle ABP$中$AB$边上的高，已知$y_{P}=3$，根据三角形面积公式$S=\frac{1}{2}\times底\times高$，可得$S_{\triangle ABP}=\frac{1}{2}\times AB\times\vert y_{P}\vert=\frac{1}{2}\times\frac{9}{2}\times3=\frac{27}{4}$。
### $(3)$求$a$的值
已知直线$x = a$与直线$l_{1},l_{2}$分别交于点$C$，$D$。
将$x = a$代入$y = 2x + 1$得$y_{C}=2a + 1$；将$x = a$代入$y=-x + 4$得$y_{D}=-a + 4$。
因为线段$CD$的长为$4$，所以$\vert y_{C}-y_{D}\vert = 4$，即$\vert(2a + 1)-(-a + 4)\vert = 4$。
则$\vert3a - 3\vert = 4$，可得到两个方程：
$3a-3 = 4$，移项可得$3a=4 + 3=7$，解得$a=\frac{7}{3}$。
$3a-3=-4$，移项可得$3a=-4 + 3=-1$，解得$a=-\frac{1}{3}$。
【答案】：
$(1)$$b = 3$，方程组的解为$\boldsymbol{\begin{cases}x = 1\\y = 3\end{cases}}$；
$(2)$$\boldsymbol{\frac{27}{4}}$；
$(3)$$\boldsymbol{a=\frac{7}{3}}$或$\boldsymbol{a = -\frac{1}{3}}$。

11. 随着大陆惠及台胞政策措施的落实,台湾水果进入了大陆市场,一水果经销商购进了A,B两种台湾水果各10箱,分配给他的甲,乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如表:

有两种配货方案(整箱配货);
方案一:甲,乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱;
方案二:按照甲、乙两店盈利相同配货,其中A种水果甲店几箱,乙店几箱? B种水果甲店几箱,乙店几箱?
(1)如果按照方案一配货,请你计算出经销商能盈利多少元; 250元
(2)请你将方案二补充完整,写出所有结果,并将你填写的方案二与方案一做比较,得出哪一种方案盈利较多. A种水果甲店2箱，乙店8箱；B种水果甲店6箱，乙店4箱 或 A种水果甲店5箱，乙店5箱；B种水果甲店4箱，乙店6箱 或 A种水果甲店8箱，乙店2箱；B种水果甲店2箱，乙店8箱。方案一盈利较多。

答案： 【解析】：
(1)
方案一盈利计算：
A种水果盈利：$(11 + 9)\times5 = 100$（元）
B种水果盈利：$(17 + 13)\times5 = 150$（元）
总盈利：$100 + 150 = 250$（元）
(2)
设A种水果甲店$x$箱，乙店$(10 - x)$箱；B种水果甲店$y$箱，乙店$(10 - y)$箱。
根据甲、乙两店盈利相同可得：$11x + 17y = 9(10 - x) + 13(10 - y)$
化简得：$11x + 17y = 90 - 9x + 130 - 13y$
$11x + 9x + 17y + 13y = 90 + 130$
$20x + 30y = 220$
$2x + 3y = 22$
因为$x$、$y$为非负整数且$x\leqslant10$，$y\leqslant10$，$10 - x\geqslant0$，$10 - y\geqslant0$。
当$x = 2$时，$y = 6$；当$x = 5$时，$y = 4$；当$x = 8$时，$y = 2$。
方案二盈利计算：
当$x = 2$，$y = 6$时，盈利$2\times11 + 6\times17 + 8\times9 + 4\times13 = 22 + 102 + 72 + 52 = 248$（元）
当$x = 5$，$y = 4$时，盈利$5\times11 + 4\times17 + 5\times9 + 6\times13 = 55 + 68 + 45 + 78 = 246$（元）
当$x = 8$，$y = 2$时，盈利$8\times11 + 2\times17 + 2\times9 + 8\times13 = 88 + 34 + 18 + 104 = 244$（元）
【答案】：
(1)$250$元
(2)方案二：A种水果甲店$2$箱，乙店$8$箱；B种水果甲店$6$箱，乙店$4$箱 或 A种水果甲店$5$箱，乙店$5$箱；B种水果甲店$4$箱，乙店$6$箱 或 A种水果甲店$8$箱，乙店$2$箱；B种水果甲店$2$箱，乙店$8$箱。方案一盈利较多。