第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
6. 若函数 $ y = ( k - 2 ) x + 2 k + 1 $ 是正比例函数,则k的值是 (
A. $ k \neq 2 $
B. $ k = 2 $
C. $ k = - \frac { 1 } { 2 } $
D. $ k = - 2 $
C
)A. $ k \neq 2 $
B. $ k = 2 $
C. $ k = - \frac { 1 } { 2 } $
D. $ k = - 2 $
答案:
C
7. 要使函数 $ y = 2 x ^ { n - 1 } + 3 $ 是一次函数,则n的值为
2
。
答案:
2
8. 写出下列各题中x与y之间的关系式,并判断y是否为x的一次函数,是否为正比例函数。
(1)已知12支铅笔,售价2.4元,销售x(支)铅笔,写出铅笔的总售价 $ y ( \mathrm { 元 } ) $ 与铅笔支数x(支)之间的关系;
(2)地面温度为 $ 12 ^ { \circ } \mathrm { C } $,如果高度每升高1km,气温下降 $ 6 ^ { \circ } \mathrm { C } $,气温 $ t ( ^ { \circ } \mathrm { C } ) $ 与高度 $ h ( \mathrm { km } ) $ 之间的关系;
(3)一个长方形的面积是 $ 16 \mathrm { cm } ^ { 2 } $,它的一边长 $ y ( \mathrm { cm } ) $ 与邻边长 $ x ( \mathrm { cm } ) $ 的关系。
(1)已知12支铅笔,售价2.4元,销售x(支)铅笔,写出铅笔的总售价 $ y ( \mathrm { 元 } ) $ 与铅笔支数x(支)之间的关系;
(2)地面温度为 $ 12 ^ { \circ } \mathrm { C } $,如果高度每升高1km,气温下降 $ 6 ^ { \circ } \mathrm { C } $,气温 $ t ( ^ { \circ } \mathrm { C } ) $ 与高度 $ h ( \mathrm { km } ) $ 之间的关系;
(3)一个长方形的面积是 $ 16 \mathrm { cm } ^ { 2 } $,它的一边长 $ y ( \mathrm { cm } ) $ 与邻边长 $ x ( \mathrm { cm } ) $ 的关系。
答案:
解:
(1)$y=\frac{2.4}{12}x=0.2x$,$y$是$x$的一次函数,也是正比例函数。
(2)$t=12-6h$,$t$是$h$的一次函数,不是正比例函数。
(3)$y=\frac{16}{x}$,$y$既不是$x$的一次函数,也不是$x$的正比例函数。
(1)$y=\frac{2.4}{12}x=0.2x$,$y$是$x$的一次函数,也是正比例函数。
(2)$t=12-6h$,$t$是$h$的一次函数,不是正比例函数。
(3)$y=\frac{16}{x}$,$y$既不是$x$的一次函数,也不是$x$的正比例函数。
9. 【新趋势·项目式学习】综合与实践
【任务一】“今技融古”
了解古代漏刻和它的计时原理。上网查阅资料,学习中国古代其他计时方法和它们的计时原理,体会中国古代文化的博大精深。
【任务二】“古物新做”
利用日常生活中的物品,借助查阅的资料和课堂所学知识,以“1分钟”为一个时间单位,设计并制作计时工具,并讲述制作过程。
如图是学思小组制作的计时仪器,水流分别经过纸杯1,2,3最后流入纸杯4,小组同学记录了流入纸杯4的水面高度 $ h ( \mathrm { cm } ) $ 与流水时间t(min)的关系如表1,同时又记录了水的体积 $ v ( \mathrm { mL } ) $ 与流水时间t(min)的关系如表2。
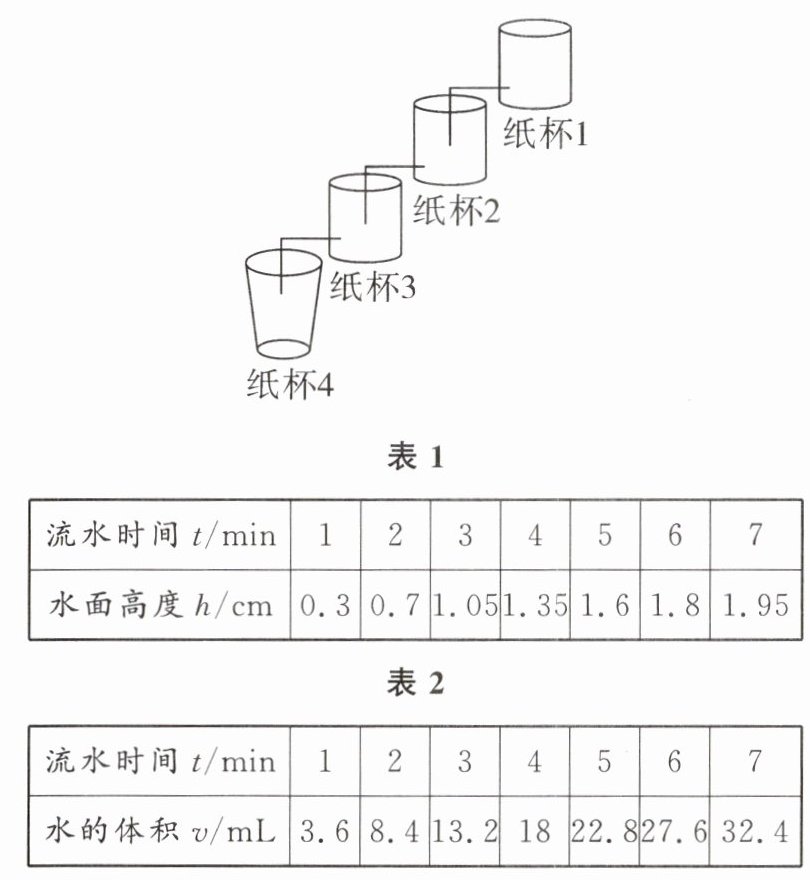
通过对表中数据的分析,小组同学发现
【任务三】“时间可见”
通过对学思小组数据的分析,为让时间“看得见”,善思小组改进了实验装置,将水的体积直接转化为仪表盘的刻度,小组同学记录了仪表表盘刻度m与流水时间t的数据如表3。

(1)请根据表3数据求表盘刻度与流水时间的函数关系式。
(2)求经过10min,表盘刻度是多少?
【任务一】“今技融古”
了解古代漏刻和它的计时原理。上网查阅资料,学习中国古代其他计时方法和它们的计时原理,体会中国古代文化的博大精深。
【任务二】“古物新做”
利用日常生活中的物品,借助查阅的资料和课堂所学知识,以“1分钟”为一个时间单位,设计并制作计时工具,并讲述制作过程。
如图是学思小组制作的计时仪器,水流分别经过纸杯1,2,3最后流入纸杯4,小组同学记录了流入纸杯4的水面高度 $ h ( \mathrm { cm } ) $ 与流水时间t(min)的关系如表1,同时又记录了水的体积 $ v ( \mathrm { mL } ) $ 与流水时间t(min)的关系如表2。

通过对表中数据的分析,小组同学发现
水的体积$v$
与流水时间t是一次函数关系。【任务三】“时间可见”
通过对学思小组数据的分析,为让时间“看得见”,善思小组改进了实验装置,将水的体积直接转化为仪表盘的刻度,小组同学记录了仪表表盘刻度m与流水时间t的数据如表3。

(1)请根据表3数据求表盘刻度与流水时间的函数关系式。
(2)求经过10min,表盘刻度是多少?
答案:
解:【任务二】水的体积$v$;
【任务三】
(1)令表盘刻度与流水时间的函数关系式为$m=kt+b$,
有表格可以看出:流水时间每增加 1 min,表盘刻度就增加 0.4,且当流水时间为 1 min 时,表盘刻度为 0.3;
则推测流水时间为 0 时,则表盘刻度为—0.1;
因为根据表 1,$(1,0.3),(2,0.7)$满足关系式,
所以函数关系式为$m=0.4t-0.1$;
(2)当$x=10$时,$m=0.4× 10-0.1=3.9$,
所以经过 10 分钟,表盘刻度是 3.9。
【任务三】
(1)令表盘刻度与流水时间的函数关系式为$m=kt+b$,
有表格可以看出:流水时间每增加 1 min,表盘刻度就增加 0.4,且当流水时间为 1 min 时,表盘刻度为 0.3;
则推测流水时间为 0 时,则表盘刻度为—0.1;
因为根据表 1,$(1,0.3),(2,0.7)$满足关系式,
所以函数关系式为$m=0.4t-0.1$;
(2)当$x=10$时,$m=0.4× 10-0.1=3.9$,
所以经过 10 分钟,表盘刻度是 3.9。
查看更多完整答案,请扫码查看


