第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
4. 球的体积V与半径R之间的关系式为V = $\frac{4}{3}\pi R^{3}$,当球的大小发生变化时,关于π,R说法中,正确的是 (
A. R是常量
B. π是变量
C. R是自变量
D. R是因变量
C
)A. R是常量
B. π是变量
C. R是自变量
D. R是因变量
答案:
C
5. 如图所示的图象分别给出了x与y的对应关系,其中表示y是x的函数的是 (
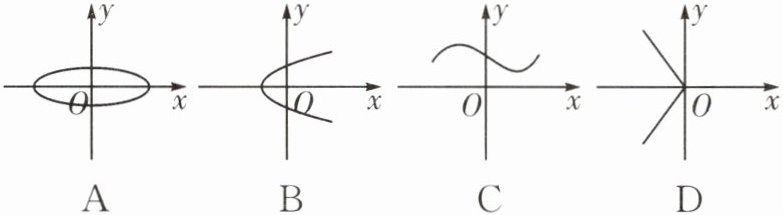
C
)
答案:
C
6. 填空:
(1) 一支圆珠笔的单价为2元,购买x支圆珠笔,总价为y元,则y =
(2) 若圆的面积为S,半径为r,则S = $\pi r^{2}$,其中常量是
(1) 一支圆珠笔的单价为2元,购买x支圆珠笔,总价为y元,则y =
2x
;在这个式子中,变量是x和y
,常量是2
,y
是x
的函数。(2) 若圆的面积为S,半径为r,则S = $\pi r^{2}$,其中常量是
π
,自变量是r
,S
是r
的函数。
答案:
(1)2x,x和y,2,y,x
(2)π,r,S,r
(1)2x,x和y,2,y,x
(2)π,r,S,r
7. 一辆汽车由北京驶往距离120km的天津,其平均速度是40km/h,则该汽车距天津的路程s(km)关于行驶时间t(h)的函数关系式及自变量的取值范围是
s=120−40t(0≤t≤3)
。
答案:
s=120−40t(0≤t≤3)
8. 一辆汽车以60km/h的速度匀速行驶,它的行驶里程为s km,行驶时间为t h。
(1) 请根据题意填写下表:

(2) 用含t的式子表示s,则s =
(3) 在(2)的式子中,自变量是
(4) 这个问题反映了匀速行驶的汽车所行驶的路程
(1) 请根据题意填写下表:

(2) 用含t的式子表示s,则s =
60t
;(3) 在(2)的式子中,自变量是
t
,因变量是s
,常量是60
,自变量的取值范围为t≥0
;(4) 这个问题反映了匀速行驶的汽车所行驶的路程
s
随行驶时间t
的变化过程。
答案:
(1)60 120 180 240 300 600
(2)60t
(3)t s 60 t≥0
(4)s t
(1)60 120 180 240 300 600
(2)60t
(3)t s 60 t≥0
(4)s t
9. 某市出租车收费按里程计算,3km以内(含3km)收费10元,超过3km,每增加1km加收2元,则当x≥3时,车费y(元)与里程x(km)之间的关系式为
y=2x+4
。
答案:
y=2x+4
10. 某机动车出发前油箱内有油48L。行驶若干小时后,途中在加油站加油若干升。油箱中剩余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答下列问题。
(1) 在这个变化过程中,
(2) 机动车行驶
(3) 如果加油站距目的地还有360km,车速为60km/h,要到达目的地,请判断油箱中的油是否够用,并说明理由。
不够用。理由如下:机动车的耗油量:(48−16)÷4=8(L/h),行驶时间360÷60=6(h),需要油量6×8=48(L),40<48,故不够用。
(1) 在这个变化过程中,
行驶时间
是自变量,剩余油量
是因变量;(2) 机动车行驶
4
h后加油,中途加油24
L;(3) 如果加油站距目的地还有360km,车速为60km/h,要到达目的地,请判断油箱中的油是否够用,并说明理由。
不够用。理由如下:机动车的耗油量:(48−16)÷4=8(L/h),行驶时间360÷60=6(h),需要油量6×8=48(L),40<48,故不够用。
答案:
解:
(1)行驶时间,剩余油量
(2)4,24
(3)不够用。理由如下:机动车的耗油量:(48−16)÷4=8(L/h),行驶时间360÷60=6(h),需要油量6×8=48(L),40<48,故不够用。
(1)行驶时间,剩余油量
(2)4,24
(3)不够用。理由如下:机动车的耗油量:(48−16)÷4=8(L/h),行驶时间360÷60=6(h),需要油量6×8=48(L),40<48,故不够用。
11. 如图,已知点A(6,0),点P(x,y)在第一象限,且x + y = 8,设△OPA的面积为S。
(1) 求S关于x的函数表达式;
(2) 求x的取值范围;
(3) 当S = 12时,求点P的坐标。
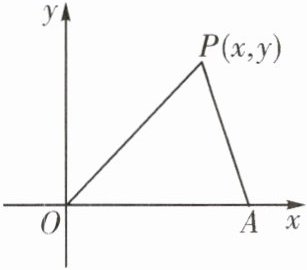
(1) 求S关于x的函数表达式;
(2) 求x的取值范围;
(3) 当S = 12时,求点P的坐标。

答案:
解:
(1)如图,过点P作PH⊥OA,则
S=$\frac{1}{2}$|OA|·|PH|
=$\frac{1}{2}$×6×y(y>0)。
因为x+y=8,
所以y=8−x,
所以S=$\frac{1}{2}$×6(8−x),
即S=24−3x。
(2)因为点P在第一象限,
所以x>0,
因为x+y=8,
所以当x=8时,y=0,不能构成三角形,
所以0<x<8。
(3)当S=12时,代入S=24−3x中,得x=4,所以点P的坐标是(4,4)。

解:
(1)如图,过点P作PH⊥OA,则
S=$\frac{1}{2}$|OA|·|PH|
=$\frac{1}{2}$×6×y(y>0)。
因为x+y=8,
所以y=8−x,
所以S=$\frac{1}{2}$×6(8−x),
即S=24−3x。
(2)因为点P在第一象限,
所以x>0,
因为x+y=8,
所以当x=8时,y=0,不能构成三角形,
所以0<x<8。
(3)当S=12时,代入S=24−3x中,得x=4,所以点P的坐标是(4,4)。

查看更多完整答案,请扫码查看


