第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
4. 如图是小明探索直线平行的条件时所用的学具,木条a,b,c在同一平面内,经测量$∠1= 70^{\circ }$,要使木条$a// b$,则$∠2$的度数应为(
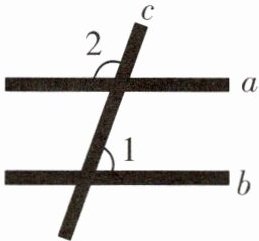
A. $20^{\circ }$
B. $70^{\circ }$
C. $110^{\circ }$
D. $160^{\circ }$
C
)
A. $20^{\circ }$
B. $70^{\circ }$
C. $110^{\circ }$
D. $160^{\circ }$
答案:
C
5. 下列图形中,由$∠1= ∠2$,能得到$AB// CD$的是(
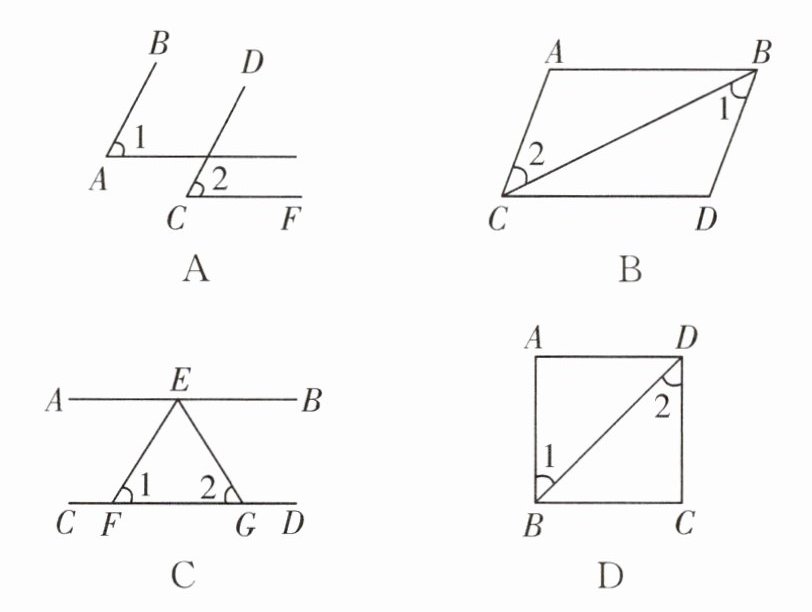
D
)
答案:
D
6. 如图,一个由4条线段构成的“鱼”形图案,其中$∠1= 50^{\circ },∠2= 50^{\circ },∠3= 130^{\circ }$,找出图中的平行线
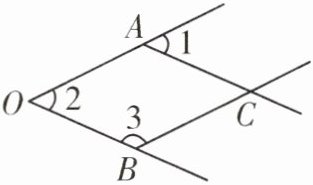
理由:$ \because \angle 1 = 50 ^ { \circ } $,$ \angle 2 = 50 ^ { \circ } $,$ \therefore \angle 1 = \angle 2 $,$ \therefore OB // AC $,$ \because \angle 2 = 50 ^ { \circ } $,$ \angle 3 = 130 ^ { \circ } $,$ \therefore \angle 2 + \angle 3 = 180 ^ { \circ } $,$ \therefore OA // BC $。
OA//BC,OB//AC
,并说明理由。
理由:$ \because \angle 1 = 50 ^ { \circ } $,$ \angle 2 = 50 ^ { \circ } $,$ \therefore \angle 1 = \angle 2 $,$ \therefore OB // AC $,$ \because \angle 2 = 50 ^ { \circ } $,$ \angle 3 = 130 ^ { \circ } $,$ \therefore \angle 2 + \angle 3 = 180 ^ { \circ } $,$ \therefore OA // BC $。
答案:
解:$ OA // BC $,$ OB // AC $。
$ \because \angle 1 = 50 ^ { \circ } $,$ \angle 2 = 50 ^ { \circ } $,
$ \therefore \angle 1 = \angle 2 $,
$ \therefore OB // AC $,
$ \because \angle 2 = 50 ^ { \circ } $,$ \angle 3 = 130 ^ { \circ } $,
$ \therefore \angle 2 + \angle 3 = 180 ^ { \circ } $,
$ \therefore OA // BC $。
$ \because \angle 1 = 50 ^ { \circ } $,$ \angle 2 = 50 ^ { \circ } $,
$ \therefore \angle 1 = \angle 2 $,
$ \therefore OB // AC $,
$ \because \angle 2 = 50 ^ { \circ } $,$ \angle 3 = 130 ^ { \circ } $,
$ \therefore \angle 2 + \angle 3 = 180 ^ { \circ } $,
$ \therefore OA // BC $。
7. 如图,$∠ABC= ∠ADC$,BE,DF分别是$∠ABC,∠ADC$的角平分线,且$∠2= ∠3$,求证:$BC// AD$。
证明:$ \because BE $,$ DF $分别是$ \angle ABC $和$ \angle ADC $的平分线,
$ \therefore \angle 1 = \frac { 1 } { 2 } \angle ABC $,$ \angle 2 = \frac { 1 } { 2 } \angle ADC $,
$ \because \angle ABC = \angle ADC $,
$ \therefore \angle 1 = \angle 2 $,
$ \because \angle 2 = \angle 3 $,
$ \therefore \angle 1 = \angle 3 $,
$ \therefore BC // AD $。
证明:$ \because BE $,$ DF $分别是$ \angle ABC $和$ \angle ADC $的平分线,
$ \therefore \angle 1 = \frac { 1 } { 2 } \angle ABC $,$ \angle 2 = \frac { 1 } { 2 } \angle ADC $,
$ \because \angle ABC = \angle ADC $,
$ \therefore \angle 1 = \angle 2 $,
$ \because \angle 2 = \angle 3 $,
$ \therefore \angle 1 = \angle 3 $,
$ \therefore BC // AD $。
答案:
证明:$ \because BE $,$ DF $分别是$ \angle ABC $和$ \angle ADC $的平分线,
$ \therefore \angle 1 = \frac { 1 } { 2 } \angle ABC $,$ \angle 2 = \frac { 1 } { 2 } \angle ADC $,
$ \because \angle ABC = \angle ADC $,
$ \therefore \angle 1 = \angle 2 $,
$ \because \angle 2 = \angle 3 $,
$ \therefore \angle 1 = \angle 3 $,
$ \therefore BC // AD $。
$ \therefore \angle 1 = \frac { 1 } { 2 } \angle ABC $,$ \angle 2 = \frac { 1 } { 2 } \angle ADC $,
$ \because \angle ABC = \angle ADC $,
$ \therefore \angle 1 = \angle 2 $,
$ \because \angle 2 = \angle 3 $,
$ \therefore \angle 1 = \angle 3 $,
$ \therefore BC // AD $。
8. 如图,下列条件中,能判定$DE// AC$的是(
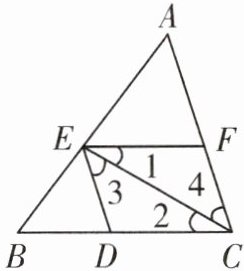
A. $∠EDC= ∠EFC$
B. $∠AFE= ∠ACD$
C. $∠3= ∠4$
D. $∠1= ∠2$
C
)
A. $∠EDC= ∠EFC$
B. $∠AFE= ∠ACD$
C. $∠3= ∠4$
D. $∠1= ∠2$
答案:
C
9. 综合与实践
学习完《平行线的证明》,我们积累了一定的研究经验,李凯和张芳将一副透明三角板中的两个直角三角尺的直角顶点C按如图所示的方式叠放在一起,其中$∠A= ∠B= 45^{\circ },$$∠D= 30^{\circ },∠E= 60^{\circ }$。
(1)操作判断
若$∠DCB= 55^{\circ }$,则$∠ACE= $
(2)性质探究
由(1)猜想$∠ACE与∠DCB$的数量关系,并证明你的猜想;
(3)拓展应用
当$∠BCE<180^{\circ }$且点B在直线CE的上方时,这两个三角尺存在一组边互相平行,请直接写出$∠BCE$所有可能的度数(不必说明理由)。
学习完《平行线的证明》,我们积累了一定的研究经验,李凯和张芳将一副透明三角板中的两个直角三角尺的直角顶点C按如图所示的方式叠放在一起,其中$∠A= ∠B= 45^{\circ },$$∠D= 30^{\circ },∠E= 60^{\circ }$。
(1)操作判断
若$∠DCB= 55^{\circ }$,则$∠ACE= $
$125^{\circ }$
;若$∠ACE= 158^{\circ }$,则$∠DCB= $$22^{\circ }$
;(2)性质探究
由(1)猜想$∠ACE与∠DCB$的数量关系,并证明你的猜想;
(3)拓展应用
当$∠BCE<180^{\circ }$且点B在直线CE的上方时,这两个三角尺存在一组边互相平行,请直接写出$∠BCE$所有可能的度数(不必说明理由)。
$30^{\circ }$、$45^{\circ }$、$120^{\circ }$、$135^{\circ }$、$165^{\circ }$
答案:
解:
(1)$ \because \angle DCB = 55 ^ { \circ } $,$ \angle ACB = 90 ^ { \circ } $,
$ \therefore \angle ACD = 35 ^ { \circ } $,
$ \because \angle DCE = 90 ^ { \circ } $,
$ \therefore \angle ACE = 90 ^ { \circ } + 35 ^ { \circ } = 125 ^ { \circ } $;
$ \because \angle ACD = \angle ACE - 90 ^ { \circ } = 158 ^ { \circ } - 90 ^ { \circ } = 68 ^ { \circ } $,
$ \angle DCB = 90 ^ { \circ } - 68 ^ { \circ } = 22 ^ { \circ } $。
故答案为:$ 125 ^ { \circ } $,$ 22 ^ { \circ } $。
(2)猜想:$ \angle ACE + \angle DCB = 180 ^ { \circ } $。
理由如下:$ \because \angle ACD = 90 ^ { \circ } - \angle DCB $,
又$ \because \angle BCE = 90 ^ { \circ } - \angle DCB $,
$ \therefore \angle ACE = \angle ACD + \angle BCE + \angle DCB $
$ = 90 ^ { \circ } - \angle DCB + 90 ^ { \circ } - \angle DCB + \angle DCB $
$ = 180 ^ { \circ } - \angle DCB $,
即$ \angle ACE + \angle DCB = 180 ^ { \circ } $。
(3)存在,$ 30 ^ { \circ } $、$ 45 ^ { \circ } $、$ 120 ^ { \circ } $、$ 135 ^ { \circ } $、$ 165 ^ { \circ } $。
理由:当$ CB // DE $时,$ \angle BCE = 120 ^ { \circ } $;
当$ AC // DE $时,$ \angle BCE = 30 ^ { \circ } $;
当$ AB // DE $时,$ \angle BCE = 165 ^ { \circ } $;
当$ AB // CD $时,$ \angle BCE = 135 ^ { \circ } $;
当$ AB // CE $时,$ \angle BCE = 45 ^ { \circ } $。
(1)$ \because \angle DCB = 55 ^ { \circ } $,$ \angle ACB = 90 ^ { \circ } $,
$ \therefore \angle ACD = 35 ^ { \circ } $,
$ \because \angle DCE = 90 ^ { \circ } $,
$ \therefore \angle ACE = 90 ^ { \circ } + 35 ^ { \circ } = 125 ^ { \circ } $;
$ \because \angle ACD = \angle ACE - 90 ^ { \circ } = 158 ^ { \circ } - 90 ^ { \circ } = 68 ^ { \circ } $,
$ \angle DCB = 90 ^ { \circ } - 68 ^ { \circ } = 22 ^ { \circ } $。
故答案为:$ 125 ^ { \circ } $,$ 22 ^ { \circ } $。
(2)猜想:$ \angle ACE + \angle DCB = 180 ^ { \circ } $。
理由如下:$ \because \angle ACD = 90 ^ { \circ } - \angle DCB $,
又$ \because \angle BCE = 90 ^ { \circ } - \angle DCB $,
$ \therefore \angle ACE = \angle ACD + \angle BCE + \angle DCB $
$ = 90 ^ { \circ } - \angle DCB + 90 ^ { \circ } - \angle DCB + \angle DCB $
$ = 180 ^ { \circ } - \angle DCB $,
即$ \angle ACE + \angle DCB = 180 ^ { \circ } $。
(3)存在,$ 30 ^ { \circ } $、$ 45 ^ { \circ } $、$ 120 ^ { \circ } $、$ 135 ^ { \circ } $、$ 165 ^ { \circ } $。
理由:当$ CB // DE $时,$ \angle BCE = 120 ^ { \circ } $;
当$ AC // DE $时,$ \angle BCE = 30 ^ { \circ } $;
当$ AB // DE $时,$ \angle BCE = 165 ^ { \circ } $;
当$ AB // CD $时,$ \angle BCE = 135 ^ { \circ } $;
当$ AB // CE $时,$ \angle BCE = 45 ^ { \circ } $。
查看更多完整答案,请扫码查看


