第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
6. 如图,在$\triangle ABC$中,$BD平分\angle ABC$,如果$AB= 8$,$BC= 12$,$\triangle ABD的面积为16$,则$\triangle CBD$的面积为______.
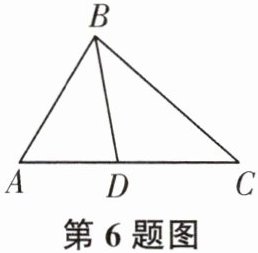



答案:
24
7. 如图,在$\triangle ABC$中,$S_{\triangle ABC}= 21$,$\angle BAC的平分线AD交BC于点D$,点$E为AD$的中点.连接$BE$,点$F为BE$上一点,且$BF= 2EF$.若$S_{\triangle DEF}= 2$,则$AB:AC= $______.



答案:
4:3
8. 如图,$CD为\text{Rt}\triangle ABC$斜边上的高,$\angle BAC的平分线分别交CD$,$BC于点E$,$F$,$FG\perp AB$,垂足为点$G$.
(1)求证:$CE= FG$;
(2)若$AC= 12$,$AB= 15$,$CE= 4$,求$\triangle ABC$的面积.
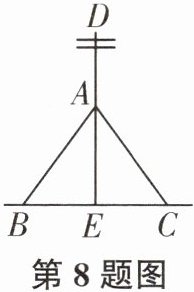


(1)求证:$CE= FG$;
(2)若$AC= 12$,$AB= 15$,$CE= 4$,求$\triangle ABC$的面积.



答案:
(1)证明:
∵AF是∠BAC的平分线,∠ACB=90°,FG⊥AB,
∴FC=FG,∠CAF=∠DAE=$\frac{1}{2}$∠BAC,
∠CAF+∠CFA=90°,∠DAE+∠AED=90°,
∴∠AED=∠AFC,
∵∠AED=∠CEF,
∴∠CEF=∠AFC,
∴CE=CF,
∴CE=FG.
(2)解:
∵CE=4,
∴FG=CF=CE=4,
∵AC=12,AB=15,
∴S△ABC=S△ACF+S△ABF=$\frac{1}{2}$AC·CF+$\frac{1}{2}$AB·FG =$\frac{1}{2}$×12×4+$\frac{1}{2}$×15×4=54,
所以△ABC的面积为54.
(1)证明:
∵AF是∠BAC的平分线,∠ACB=90°,FG⊥AB,
∴FC=FG,∠CAF=∠DAE=$\frac{1}{2}$∠BAC,
∠CAF+∠CFA=90°,∠DAE+∠AED=90°,
∴∠AED=∠AFC,
∵∠AED=∠CEF,
∴∠CEF=∠AFC,
∴CE=CF,
∴CE=FG.
(2)解:
∵CE=4,
∴FG=CF=CE=4,
∵AC=12,AB=15,
∴S△ABC=S△ACF+S△ABF=$\frac{1}{2}$AC·CF+$\frac{1}{2}$AB·FG =$\frac{1}{2}$×12×4+$\frac{1}{2}$×15×4=54,
所以△ABC的面积为54.
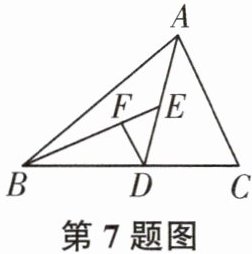
9. 如图,在$\triangle ABC$中,$AD平分\angle BAC$,$\angle C= 90^{\circ}$,$DE\perp AB$,垂足为$E$,点$F在AC$上,$BD= DF$.
(1)求证:$CF= EB$;
(2)若$AB= 12$,$AF= 8$,求$CF$的长.
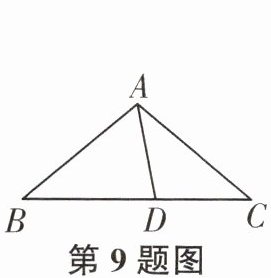

(1)求证:$CF= EB$;
(2)若$AB= 12$,$AF= 8$,求$CF$的长.



答案:
(1)证明:
∵AD平分∠BAC,∠C =90°,DE⊥AB于E,

∴DE=DC.
在Rt△CDF与Rt△EDB中,
$ \left\{ \begin{array} { l } { D F = D B } \\ { D C = D E } \end{array} \right. $
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
(2)解:设CF=x,则AE=12−x,
∵AD平分∠BAC,DE⊥AB,
∴CD=DE.
在Rt△ACD与Rt△AED中,
$ \left\{ \begin{array} { l } { A D = A D } \\ { C D = D E } \end{array} \right. $
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,即8+x=12−x,
解得x=2,即CF=2.
(1)证明:
∵AD平分∠BAC,∠C =90°,DE⊥AB于E,

∴DE=DC.
在Rt△CDF与Rt△EDB中,
$ \left\{ \begin{array} { l } { D F = D B } \\ { D C = D E } \end{array} \right. $
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
(2)解:设CF=x,则AE=12−x,
∵AD平分∠BAC,DE⊥AB,
∴CD=DE.
在Rt△ACD与Rt△AED中,
$ \left\{ \begin{array} { l } { A D = A D } \\ { C D = D E } \end{array} \right. $
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,即8+x=12−x,
解得x=2,即CF=2.
10. 【新情境】
图$1$是一个平分角的仪器,其中$OD= OE$,$FD= FE$.

(1)如图$2$,将仪器放置在$\triangle ABC$上,使点$O与顶点A$重合,$D$,$E分别在边AB$,$AC$上,沿$AF画一条射线AP$,交$BC于点P$.$AP是\angle BAC$的平分线吗? 请判断并说明理由;
(2)如图$3$,在(1)的条件下,过点$P作PQ\perp AB于点Q$,若$PQ= 4$,$AC= 6$,求$\triangle APC$的面积.


图$1$是一个平分角的仪器,其中$OD= OE$,$FD= FE$.

(1)如图$2$,将仪器放置在$\triangle ABC$上,使点$O与顶点A$重合,$D$,$E分别在边AB$,$AC$上,沿$AF画一条射线AP$,交$BC于点P$.$AP是\angle BAC$的平分线吗? 请判断并说明理由;
(2)如图$3$,在(1)的条件下,过点$P作PQ\perp AB于点Q$,若$PQ= 4$,$AC= 6$,求$\triangle APC$的面积.


答案:
解:
(1)AP是∠BAC的平分线,理由如下:
在△ADF和△AEF中,
$ \left\{ \begin{array} { l } { A D = A E } \\ { A F = A F } \\ { D F = E F } \end{array} \right. $
∴△ADF≌△AEF(SSS),
∴∠DAF=∠EAF,
∴AP平分∠BAC;
(2)如图,过点P作PM⊥AC于点M,

∵AP平分∠BAC,PQ⊥AB,
∴PM=PQ=4,
∴S△APC=$\frac{1}{2}$AC·PM=$\frac{1}{2}$×6×4=12.
解:
(1)AP是∠BAC的平分线,理由如下:
在△ADF和△AEF中,
$ \left\{ \begin{array} { l } { A D = A E } \\ { A F = A F } \\ { D F = E F } \end{array} \right. $
∴△ADF≌△AEF(SSS),
∴∠DAF=∠EAF,
∴AP平分∠BAC;
(2)如图,过点P作PM⊥AC于点M,

∵AP平分∠BAC,PQ⊥AB,
∴PM=PQ=4,
∴S△APC=$\frac{1}{2}$AC·PM=$\frac{1}{2}$×6×4=12.
查看更多完整答案,请扫码查看


