第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1. 点$M(a,5)与点N(-3,b)$关于原点对称,则点$(a,b)$所在的象限是 ()
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
答案:
D
2. 在平面直角坐标系中,平行四边形$ABCD中点A的坐标是(0,2)$,现将平行四边形$ABCD$平移,使点$A落在点A'(5,-1)$处,则此平移可以是 ()
A. 先向右平移5个单位长度,再向下平移1个单位长度
B. 先向右平移5个单位长度,再向下平移3个单位长度
C. 先向右平移4个单位长度,再向下平移1个单位长度
D. 先向右平移4个单位长度,再向下平移3个单位长度
A. 先向右平移5个单位长度,再向下平移1个单位长度
B. 先向右平移5个单位长度,再向下平移3个单位长度
C. 先向右平移4个单位长度,再向下平移1个单位长度
D. 先向右平移4个单位长度,再向下平移3个单位长度
答案:
B
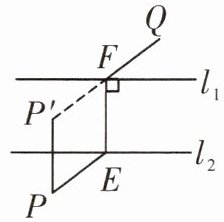
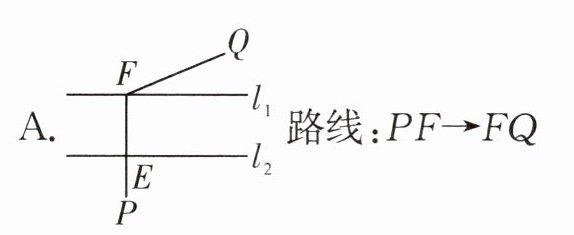
3. 如图,直线$l_{1},l_{2}$表示一条河的两岸,且$l_{1}// l_{2}$. 现要在这条河上建一座桥(桥与河的两岸相互垂直),使得从村庄$P经桥过河到村庄Q$的路程最短,应该选择路线 ()
A.
B. 路线:PE→
EQ
C. 路线:PE→EF→FQ
D. 路线:PE→EF→FQ
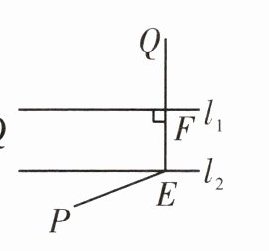

A.
B. 路线:PE→

EQ
C. 路线:PE→EF→FQ
D. 路线:PE→EF→FQ



答案:
C
4. 如图,在$Rt\triangle ABC$中,$AB= AC$,$D$,$E是斜边BC$上两点,且$∠DAE= 45^{\circ}$,将$\triangle ADC绕点A顺时针旋转90^{\circ}$后,得到$\triangle AFB$,连接$EF$,下列结论:①$\triangle AED\cong \triangle AEF$;②$BF= DE$;③$BE+DC= DE$;④$BE^{2}+DC^{2}= DE^{2}$,其中正确的结论有______个.


答案:
解:
∵AB=AC,∠BAC=90°,
∴∠ABC=∠C=45°,
∵△ADC绕点A顺时针旋转90°后,得到△AFB,
∴AD=AF,BF=CD,∠FAD=90°,△ADC≌△ABF,
∵∠DAE=45°,
∴∠FAE=45°,
在△AED和△AEF中,
$\left\{\begin{array}{l} AD=AF\\ \angle FAE=\angle DAE\\ AE=AE\end{array}\right.$
∴△AED≌△AEF(SAS),所以①正确;
∴EF=DE,
∵△ADC≌△ABF,
∴∠ABF=∠C=45°,
∴∠FBE=45°+45°=90°,
∴EF>BE,
∴DE>BE;所以②错误;
∵BF+BE>EF,
而BF=CD,
∴BE+CD>DE,所以③错误;
∵∠FBE=90°,
∴BE²+BF²=EF²,
∴BE²+CD²=DE²,所以④正确.
故答案为:2.
∵AB=AC,∠BAC=90°,
∴∠ABC=∠C=45°,
∵△ADC绕点A顺时针旋转90°后,得到△AFB,
∴AD=AF,BF=CD,∠FAD=90°,△ADC≌△ABF,
∵∠DAE=45°,
∴∠FAE=45°,
在△AED和△AEF中,
$\left\{\begin{array}{l} AD=AF\\ \angle FAE=\angle DAE\\ AE=AE\end{array}\right.$
∴△AED≌△AEF(SAS),所以①正确;
∴EF=DE,
∵△ADC≌△ABF,
∴∠ABF=∠C=45°,
∴∠FBE=45°+45°=90°,
∴EF>BE,
∴DE>BE;所以②错误;
∵BF+BE>EF,
而BF=CD,
∴BE+CD>DE,所以③错误;
∵∠FBE=90°,
∴BE²+BF²=EF²,
∴BE²+CD²=DE²,所以④正确.
故答案为:2.
5. 如图,在$\triangle ABC$中,$∠BAC= 45^{\circ}$,$∠ACB= 30^{\circ}$,将$\triangle ABC绕点A顺时针旋转得到\triangle A_{1}B_{1}C_{1}$,当$C,B_{1},C_{1}$三点共线时,旋转角为$\alpha$,连接$BB_{1}$,交$AC于点D$,则$\frac {AB}{B_{1}C}= $______.


答案:
解:过B点作BE⊥AC于E,
∵将△ABC绕点A顺时针旋转得到△A₁B₁C₁,
∴∠C₁AB₁=∠BAC=45°,
∠ACB=∠AC₁B₁=30°,AC=AC₁,

∴∠C₁AC=120°,
∴∠B₁AC=75°,
∵∠AB₁C₁=∠BAC=105°,
∴∠AB₁C=75°,
∴∠B₁AC=∠AB₁C,
∴CA=CB₁,
∵∠BAC=45°,∠ACB=30°,
∴AE=BE=$\frac{\sqrt{2}}{2}$AB,CE=$\sqrt{3}$BE,
∴CE=$\frac{\sqrt{6}}{2}$AB,
∴CB₁=AC=AE+CE=($\frac{\sqrt{2}}{2}$+$\frac{\sqrt{6}}{2}$)AB,
∴$\frac{AB}{B₁C}$=$\frac{\sqrt{6}-\sqrt{2}}{2}$;
故答案为:$\frac{\sqrt{6}-\sqrt{2}}{2}$.
解:过B点作BE⊥AC于E,
∵将△ABC绕点A顺时针旋转得到△A₁B₁C₁,
∴∠C₁AB₁=∠BAC=45°,
∠ACB=∠AC₁B₁=30°,AC=AC₁,

∴∠C₁AC=120°,
∴∠B₁AC=75°,
∵∠AB₁C₁=∠BAC=105°,
∴∠AB₁C=75°,
∴∠B₁AC=∠AB₁C,
∴CA=CB₁,
∵∠BAC=45°,∠ACB=30°,
∴AE=BE=$\frac{\sqrt{2}}{2}$AB,CE=$\sqrt{3}$BE,
∴CE=$\frac{\sqrt{6}}{2}$AB,
∴CB₁=AC=AE+CE=($\frac{\sqrt{2}}{2}$+$\frac{\sqrt{6}}{2}$)AB,
∴$\frac{AB}{B₁C}$=$\frac{\sqrt{6}-\sqrt{2}}{2}$;
故答案为:$\frac{\sqrt{6}-\sqrt{2}}{2}$.
查看更多完整答案,请扫码查看


