第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
6. 如图,为一副重叠放置的三角板,其中∠ABC= ∠EDF= 90°,BC与DF共线,将△DEF沿CB方向平移,当EF经过AC的中点O时,直线EF交AB于点G,若BC= 4,则此时OG的长度为()
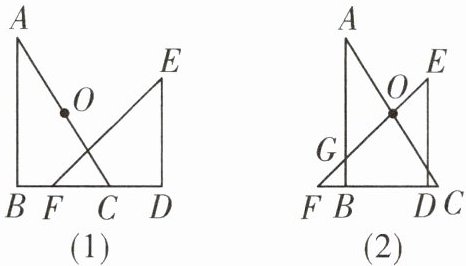
A. 3
B. 4
C. 2√2
D. $\frac{3\sqrt{2}}{2}$
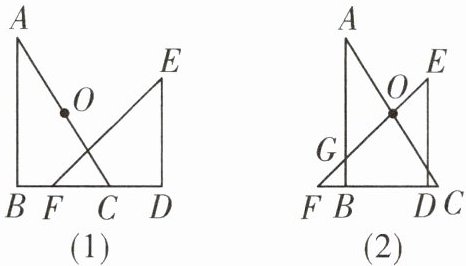
A. 3
B. 4
C. 2√2
D. $\frac{3\sqrt{2}}{2}$
答案:
C
7. 如图,在长为14,宽为10的矩形内部,沿平行于矩形各边的方向分割出三个小矩形,则三个小矩形的周长之和是______.
答案:
48
8. 如图,点A,C的坐标分别为(-2,4),(4,0),将三角形AOC沿x轴向右平移,得到三角形BDE,已知DC= 1,则点B的坐标为______.
答案:
(1,4)
9. 如图1,在长方形的草坪上有两条等宽且互相垂直的长方形小路,为求草坪面积,我们进行了如图2所示的平移变换,那么你能求出草坪的面积吗?


答案:
解:草坪的面积为(50 - 2)(30 - 2)=1344(m²).
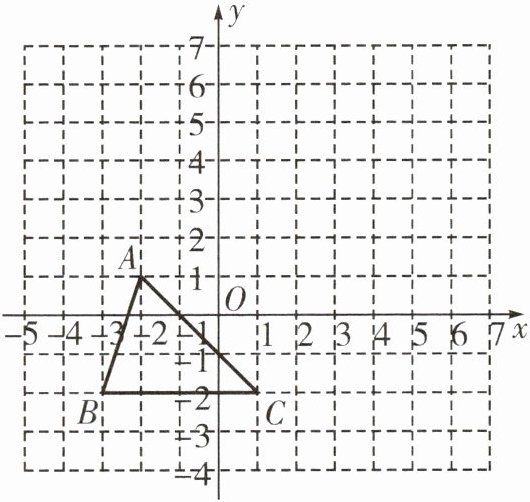
10. 如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A'B'C'.
(1)画出△A'B'C'并写出A',B',C'的坐标;
(2)求出△ABC的面积;
(3)若点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
(1)画出△A'B'C'并写出A',B',C'的坐标;
(2)求出△ABC的面积;
(3)若点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.

答案:
解:
(1)△A'B'C'如图所示:A'(0,4),B'(-1,1),C'(3,1).

(2)S△ABC = $\frac{1}{2}$×(3 + 1)×3 = 6.
(3)设点P的坐标为(0,y),
∵BC = 4,点P到BC的距离为|y + 2|,
由题意得$\frac{1}{2}$×4×|y + 2| = 6,解得y = 1或y = -5,
∴点P的坐标为(0,1)或(0,-5).
解:
(1)△A'B'C'如图所示:A'(0,4),B'(-1,1),C'(3,1).

(2)S△ABC = $\frac{1}{2}$×(3 + 1)×3 = 6.
(3)设点P的坐标为(0,y),
∵BC = 4,点P到BC的距离为|y + 2|,
由题意得$\frac{1}{2}$×4×|y + 2| = 6,解得y = 1或y = -5,
∴点P的坐标为(0,1)或(0,-5).
11. 如图,△ABC是等边三角形,将△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于点F.猜想AC与BD的位置关系,并证明你的结论.


答案:
解:AC⊥BC.证明:
∵△DCE由△ABC平移而成,
∴△DCE≌△ABC,
∴△DCE是等边三角形,
∴BC = CD,∠ACB = ∠DCE = 60°,
∴∠ACD = 180° - 120° = 60°,
∴∠ACD = ∠ACB.
∵BC = CD,
∴AC⊥BD.
∵△DCE由△ABC平移而成,
∴△DCE≌△ABC,
∴△DCE是等边三角形,
∴BC = CD,∠ACB = ∠DCE = 60°,
∴∠ACD = 180° - 120° = 60°,
∴∠ACD = ∠ACB.
∵BC = CD,
∴AC⊥BD.
查看更多完整答案,请扫码查看


