《2025年春如金卷数学暑假作业本八年级》

5. 若$//ogram ABCD的周长为30\mathrm{cm}$,$BC= 10\mathrm{cm}$,则$AB$的长是______$\mathrm{cm}$.

答案： 5

6. 在四边形$ABCD$中,若$AB// CD$,且$AD// BC$,则四边形$ABCD$叫做平行四边形.若一个平行四边形的三个顶点的坐标分别是$(2,5)$,$(3,0)$,$(1,3)$,且第四个顶点在第四象限,则第四个顶点的坐标是______.

答案： $(2,−2)$

7. 如图,$//ogram ABCD的两条对角线AC与BD相交于点O$,且$AC⊥AB$,已知$AC= 10$,$BD= 26$,那么$//ogram ABCD$的面积为______.

答案： 120

8. 如图,在$//ogram ABCD$中,$BF平分∠ABC$,交$AD于点F$,$CE平分∠BCD$,交$AD于点E$,$AB= 6$,$EF= 2$,则$BC$长为______.

答案：
10　解:
∵四边形ABCD是平行四边形，
∴AD//BC,DC=AB=6,AD =BC,
∴∠AFB=∠FBC,
∵BF平分∠ABC,
∴∠ABF=∠FBC,
则∠ABF=∠AFB,
∴AF=AB=6,
同理可证:DE=DC=6,
∵EF=AF+DE−AD=2,
即6+6−AD=2,
解得:AD=10;
∴BC=10;
故答案为:10.

9. 如图所示,在平行四边形$ABCD$中,$AE⊥BC$,垂足为$E$,$AF⊥CD$,垂足为$F$,$∠BAD= 120^{\circ}$,$BE= 2$,$FD= 3$,
(1)求$∠EAF$的度数;
(2)求平行四边形$ABCD$的周长.

答案： 解:
(1)
∵四边形ABCD是平行四边形，∠BAD=120°,
∴AD//BC,∠B=∠D,
∴∠B+∠BAD=180°,
∴∠B=180°−120°=60°,
∴∠B=∠D=60°,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°
∴∠BAE=∠DAF=30°,
∴∠EAF=∠BAD−∠BAE−∠DAF=60°;
(2)
∵四边形ABCD是平行四边形，
∴AB=CD,AD=BC,
∵∠BAE=∠DAF=30°,
∴AB=2BE,AD=2DF,
∵BE=2,FD=3,
∴AB=4,AD=6,
∴平行四边形ABCD的周长为2(AB+AD)=2×(4 +6)=20.

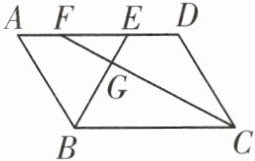
10. 如图,在$//ogram ABCD$中,$∠ABC的平分线交AD于点E$,$∠BCD的平分线交AD于点F$,交$BE于点G$.
(1)求证:$AF= DE$;
(2)若$AD= 16$,$EF= 12$,请求出$//ogram ABCD$的周长.

答案：
(1)证明:
∵四边形ABCD是平行四边形，
∴AD//BC,AB=CD,
∴∠AEB=∠CBE,
∵BE是∠ABC的平分线，
∴∠ABE=∠CBE=$\frac{1}{2}$∠ABC,
∴∠ABE=∠AEB,
∴AE=AB,
同理可得:DF=CD,
∴AE=DF,
∴AE−EF=DF−EF,
∴AF=DE;
(2)解:
∵AD=16,
∴AF+EF+DE=16,
∵AF=DE,EF=12,
∴AF+12+AF=16,
解得AF=2,
∴AB=AE=AF+EF=2+12=14,
∴▱ABCD的周长为2(AB+AD)=2×(16+14)=60,即▱ABCD的周长为60.

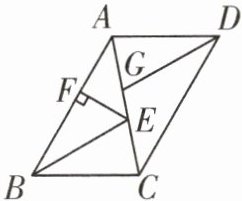
11. 如图,在$//ogram ABCD$中,$BE$,$DG分别平分∠ABC$,$∠ADC$,交$AC于点E$,$G$.
(1)求证:$△AGD≌△CEB$;
(2)过点$E作EF⊥AB$,垂足为$F$.若平行四边形$ABCD的周长为48$,$EF= 8$,求$//ogram ABCD$的面积.

答案：

(1)证明:
∵BE、DG分别平分∠ABC、∠ADC,交AC于点E、G，
∴∠ADG=$\frac{1}{2}$∠ADC,∠CBE=$\frac{1}{2}$∠ABC,
∵四边形ABCD是平行四边形，
∴∠ADC=∠ABC,AD//CB,AD=CB,
∴∠ADG=∠CBE,∠DAG=∠BCE,
在△AGD和△CEB中，
$\begin{cases}∠ADG = ∠CBE \\ AD = CB \\ ∠DAG = ∠BCE\end{cases}$
∴△AGD≌△CEB(ASA).
(2)解:作EH⊥BC于点H，
∵BE分别平分∠ABC,EF⊥AB于点F，
∴EH=EF=8,
∵AB=CD,BC=DA,且平行四边形ABCD的周长为48，
∴2AB+2BC=48,
∴AB+BC=24,
∴$S_{△ABC}=S_{△ABE}+S_{△CBE}=\frac{1}{2}AB\cdot EF+\frac{1}{2}BC\cdot EH=\frac{1}{2}×8(AB+BC)=\frac{1}{2}×8×24=96$,
在△ABC和△CDA中，
$\begin{cases}AB = CD \\ BC = DA \\ AC = CA\end{cases}$
∴△ABC≌△CDA(SSS),
∴$S_{△ABC}=S_{△CDA}=96$,
∴$S_{//ogram ABCD}=S_{△ABC}+S_{△CDA}=96+96=192$,
∴▱ABCD的面积是192.