《2025年春如金卷数学暑假作业本八年级》

11. 如图,在四边形$ABCD$中,$AC$,$BD$为对角线,$\angle ABC= \angle ACB= 60^{\circ}$,$\angle ADC= 30^{\circ}$,已知$AD= 5$,$CD= 4则BD= $______。

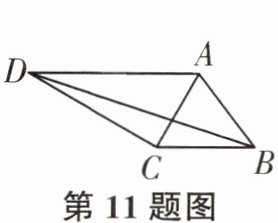
答案： $\sqrt{41}$

12. 如图,在四边形$ABCD$中,$P是对角线BD$的中点,点$E$,$F分别是AB$,$CD$的中点,$AD= BC$,$\angle EPF= 140^{\circ}$,则$\angle EFP$的度数是______。

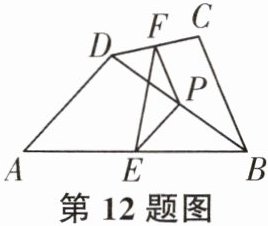
答案： 20°

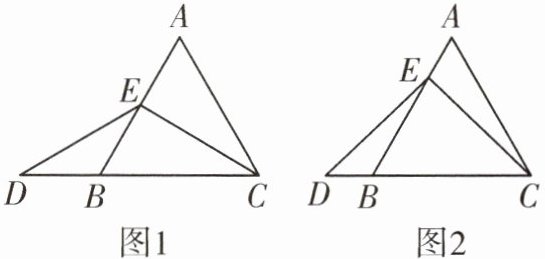
13. 在等边三角形$ABC$中,点$E在AB$边上,点$D在CB$的延长线上,且$DE= EC$。
(1)如图$1$,当$E为AB$中点时,求证：$CB= 2BD$；
(2)如图$2$,若$AB= 8$,$AE= 2$,求$CD$的长。

答案：

(1)证明:
∵△ABC为等边三角形，
　
∴∠ABC=∠A=∠ACB=60°,AC=BC,
　
∵E为AB中点，
　
∴EB=AE,
　
∴CE⊥AB,CE是∠ACB的角平分线，
　
∴∠BEC=90°,∠BCE=30°,
　
∴2EB=BC,
　
∵ED=EC,
　
∴∠EDC=∠ECD=30°,
　
∴∠DEB=60°−30°=30°,
　
∴BD=BE,
　
∴2BD=BC;
(2)解:如图2,过点E作EF//BC,交AC于点F，
　
∵△ABC为等边三角形，
　
∴∠AFE=∠ACB=∠ABC =60°,AB=BC=8,
　
∵EF//BC,
　
∴∠AEF=∠ABC=60°,∠ECB=∠FEC,
　
∴△AEF为等边三角形，
　
∴∠EFC=∠EBD=120°,EF=AE,
　
∵ED=EC,
　
∴∠EDB=∠ECB,
　
∴∠EDB=∠FEC,
　　在△BDE和△FEC中，
　　$\begin{cases}\angle EBD=\angle EFC \\\angle EDB=\angle FEC \\ED=EC\end{cases}$
　
∴△BDE≌△FEC(AAS),
　
∴BD=EF,
　
∴AE=BD=2,
　
∴CD=BC+BD=8+2=10.
　　　　　　　　　　　　　　　　

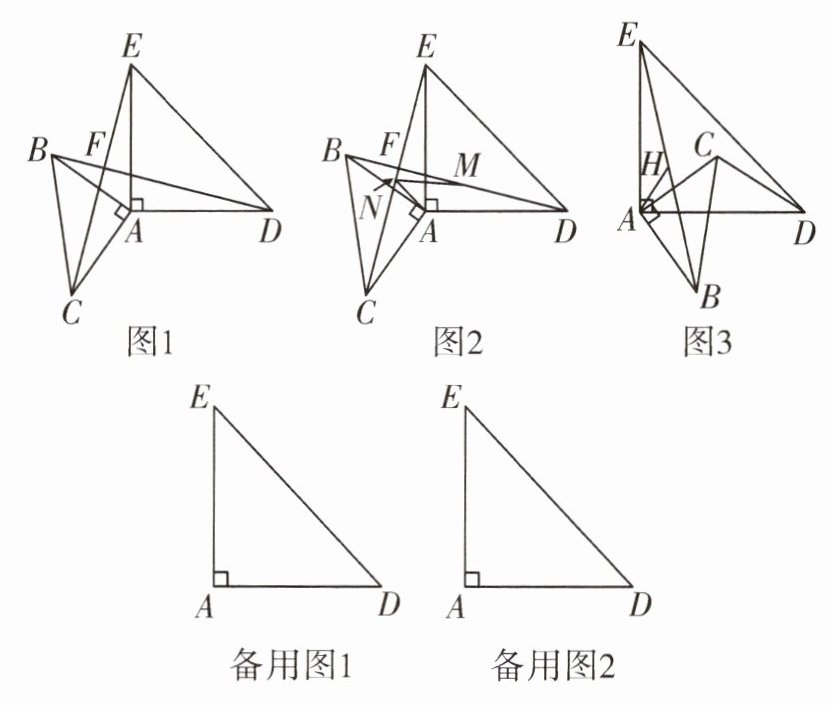
14. 问题背景：$\triangle ABC和\triangle ADE$都是等腰直角三角形,$\angle BAC= \angle DAE= 90^{\circ}$,$AB= AC$,$AD= AE$。
(1)问题探究：连接$BD与CE$,$BD与CE交点为F$。
①如图$1$,$BD与CE$的数量关系是______(填“相等”或“不相等”),$BD与CE$的位置关系是______(填“平行”或“垂直”)；
②如图$2$,$M$,$N分别是BD与CE$的中点,$\angle ANM= $______$^{\circ}$；
(2)问题拓展：当等腰直角$\triangle ABC旋转到如图3$位置,连接$BE$,$CD$,点$H为BE$中点,当$B$,$C$,$D$三点共线时,若$AB= 4$,$AD= 4\sqrt{5}$,请求出线段$AH$的长。

答案：
解:
(1)①如图1，
　　设AB与CE交于点O，
　
∵∠BAC=∠DAE=90°,AB=AC,AD=AE.
　
∴∠BAC+∠BAE=∠DAE +∠BAE,
　
∴∠CAE=∠BAD,
　
∴△CAE≌△BAD(SAS),
　
∴BD=CE,∠ACE=∠ABD,
　
∵∠BOF=∠AOC,
　
∴∠BFO=∠BAC=90°,
　
∴BD⊥CE,
　　故答案为:相等，垂直;
　　②如图2,
　　连接AM,
　　由①知，
　　∠ACE=∠ABD,CE=BD,
　
∵M、N分别是BD与CE的中点，
　
∴CN=$\frac{1}{2}$CE,BM=$\frac{1}{2}$BD,
　
∴CN=BM,
　
∵AC=AB,
　
∴△ACN≌△ABM(SAS),
　
∴AN=AM,∠CAN=∠BAM,
　
∴∠CAN−∠BAN=∠BAM−∠BAN,
　
∴∠MAN=∠BAC=90°,
　
∴∠ANM=∠AMN=45°,
　　故答案为:45;
(2)如图3,
　　当C在BD上时，
　　作AR⊥BC于R,延长AH至W,使HW=AH,
　
∴∠ARD=90°,
　
∵∠ACB=45°,∠ARC=90°,
　
∴AR=CR=$\frac{\sqrt{2}}{2}$AC=2$\sqrt{2}$,
　
∴DR=$\sqrt{AD^{2}-AR^{2}}=\sqrt{(4\sqrt{5})^{2}-(2\sqrt{2})^{2}}=6\sqrt{2}$,
　
∴CD=DR−CR=6$\sqrt{2}$−2$\sqrt{2}$=4$\sqrt{2}$,
　
∵H是BE的中点，
　
∴四边形ABWE是平行四边形，
　
∴EW=AB=AC,∠AEW+∠BAE=180°,
　
∵∠BAC+∠DAE=90°+90°=180°,
　
∴∠CAD+∠BAE=180°,
　
∴∠AEW=∠CAD,
　
∵AD=AE,
　
∴△AEW≌△ADC(SAS),
　
∴AW=CD=4$\sqrt{2}$,
　
∴AH=2$\sqrt{2}$,
　　　　　　　　　　　　　　　　　
　　如图4，
　　当点C在DB的延长线上时，
　　CD=DR+CR=6$\sqrt{2}$+2$\sqrt{2}$=8$\sqrt{2}$,
　
∴AH=$\frac{1}{2}$CD=4$\sqrt{2}$,
　　综上所述:AH=2$\sqrt{2}$或4$\sqrt{2}$.