《2025年春如金卷数学暑假作业本八年级》

3. 如图,在$\triangle ABC$中,$D为BC$上一点,$BD= 5$,$CD= 4$,$AC= AD$,则$AB^{2}-AC^{2}= $()
A. $25$
B. $29$
C. $41$
D. $45$

答案： D

4. 下列条件中,不能判定两个直角三角形全等的是()
A. 斜边和一条直角边分别相等
B. 一个锐角和斜边分别相等
C. 两条直角边分别相等
D. 两个锐角分别相等

答案： D

5. 如图,在$6× 6$的正方形网格中,每个小正方形的边长均为$1$,$\triangle ABC$的顶点均在格点上,则该三角形$AB$边上的高为()
A. $2$
B. $\frac{3\sqrt{2}}{2}$
C. $2\sqrt{2}$
D. $\frac{5}{2}$

答案： B

6. 如图每个小正方形的边长为$1$,$A$,$B$,$C$是小正方形的顶点,则$\angle ABC$的度数为()
A. $30^{\circ}$
B. $45^{\circ}$
C. $50^{\circ}$
D. $60^{\circ}$

答案： B

7. 在一个$\text{Rt}\triangle ABC$中,有一个锐角等于$25^{\circ}$,则另一个锐角的度数是______.

答案： 65°

8. 如图所示,$AB// CD$,$EF\perp BD$,垂足为$E$,$\angle 2= 60^{\circ}$,$ED= 3$,则$EF$的长为______.

答案： 3$\sqrt{3}$

9. 某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角建造了一块绿化地(阴影部分).如图,已知$AB= 9\ \text{m}$,$BC= 12\ \text{m}$,$CD= 17\ \text{m}$,$AD= 8\ \text{m}$,技术人员通过测量确定了$\angle ABC= 90^{\circ}$.则这片绿地的面积是______$\text{m}^{2}$.

答案： 114

10. 如图,在$\text{Rt}\triangle ABC$中,$AC= 6$,$BC= 8$,则其内部五个小直角三角形的周长之和为______.

答案： 24

11. 如图,$\triangle ABD和\triangle BDC$均为直角三角形,且$AD= 3$,$\angle ADB= \angle C= 60^{\circ}$,点$P从点B向点C$运动,在运动过程中,线段$DP$长的最大值为______,最小值为______,当点$P为BC$边中点时,则$DP$长为______.

答案： 6,3,2$\sqrt{3}$

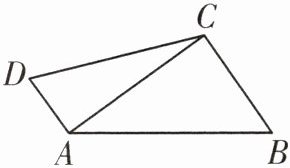
12. 如图,在四边形$ABCD$中,$\angle ACB= 90^{\circ}$,$AB= 15$,$BC= 9$,$AD= 5$,$DC= 13$.
(1)求$\angle CAD$的度数;
(2)求四边形$ABCD$的面积.

答案： 解:
(1)在Rt△ACB中,∠ACB=90°,AB=15,BC =9,
　
∴AC= $\sqrt{AB²−BC²}$=$\sqrt{15²−9²}$=12.
　
∵AD=5,CD=13,AC=12,
　
∴AD²+AC²=5²+12²=169,CD²=13²=169,
　
∴CD²=AD²+AC²,
　
∴△ACD是直角三角形，且∠CAD=90°;
(2)S△ACD=$\frac{1}{2}$AD·AC
　　=$\frac{1}{2}$×5×12
　　=30;
　　S△ABC=$\frac{1}{2}$AC·BC
　　=$\frac{1}{2}$×12×9
　　=54,
　
∴30+54=84,
　
∴四边形ABCD的面积为84.