《2025年春如金卷数学暑假作业本八年级》

1. 如图,在$//ogram ABCD$中,$AC与BD相交于点O$,延长$CD至点E$,使$DE= CD$,连接$AE$.若$∠ABD= 90^{\circ}$,$AC= 10$,$BD= 6$,则四边形$ABDE$的周长为 ()
A. $18$
B. $20$
C. $22$
D. $24$

答案： B

2. 如图,在$//ogram ABCD$中,$E$,$F分别在边AB$,$CD$上,$BE= DF$. 求证:四边形$AECF$是平行四边形. 下面是打乱顺序的证明过程,则正确的步骤排序应为 ()
①又$\because AE// CF$;
②$\because BE= DF$,$\therefore AB-BE= CD-DF$,即$AE= CF$;
③$\therefore四边形AECF$是平行四边形;
④$\therefore AB= CD$,$AB// CD$;
⑤$\because四边形ABCD$是平行四边形;
A. ④①③⑤②
B. ②④⑤①③
C. ⑤④①②③
D. ⑤④②①③

答案： D

3. 一个四边形的三个内角的度数依次如下,能判定该四边形是平行四边形的是 ()
A. $82^{\circ}$,$98^{\circ}$,$82^{\circ}$
B. $102^{\circ}$,$88^{\circ}$,$102^{\circ}$
C. $82^{\circ}$,$98^{\circ}$,$98^{\circ}$
D. $92^{\circ}$,$78^{\circ}$,$92^{\circ}$

答案： A

4. 如图,在$//ogram ABCD$中,$AB= 6\mathrm{cm}$,$BC= 12\mathrm{cm}$,$∠B= 60^{\circ}$,点$P从点A$出发,以$1\mathrm{cm}/\mathrm{s}的速度沿A→D$运动,同时点$Q从点C$出发,以$3\mathrm{cm}/\mathrm{s}的速度沿C→B$运动. 在此运动过程中,当$t= $______时,线段$PQ= CD$.

答案：
$\frac{3}{2}$或3　解:如图1,PQ=CD,且PQ与CD不平行,作CE//PQ交AD于点E，
∵四边形ABCD是平行四边形，
∴AD//BC,AB=CD=6cm,AD=BC=12cm,∠D=∠B=60°,
∴PE//CQ,
∴四边形PQCE是平行四边形，
∴CE=PQ=CD,PE=CQ,
∴△CDE是等边三角形，
∴ED=CD=6cm,
∵AP=tcm,PE=CQ=3tcm,
∴t+3t+6=12,
解得t=$\frac{3}{2}$;
如图2,PQ=CD,且PQ//CD,则四边形PQCD是平行四边形，
∴PD=CQ=3tcm,
∴t+3t=12,
解得t=3,
故答案为:$\frac{3}{2}$或3.

5. 四边形$ABCD$是一个平行四边形,$BE长是BC的长的\frac{1}{3}$,若$S_{1}$,$S_{2}$,$S_{3}$,$S分别表示△ABE$,$△CDE$,$△ADE和平行四边形ABCD$的面积,则$S_{1}:S_{2}:S_{3}:S= $______.

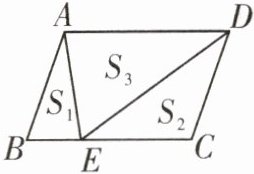
答案：
∴$S_{1}:S_{2}:S_{3}:S=1:2:3:6$

6. 如图,在四边形$ABCD$中,$∠BAC= ∠ACD= 90^{\circ}$,$∠B= ∠AEC$.
(1)求证:四边形$ABCE$是平行四边形;
(2)若$AC= 3$,$AD= 5$,点$E是CD$的中点,求$//ogram ABCE$的面积.

答案：
(1)证明:
∵∠BAC=∠ACD=90°,
∴AB//CE,
∴∠B+∠BCE=180°,
∵∠B=∠AEC,
∴∠AEC+∠BCE=180°,
∴AE//BC,
∴四边形ABCE是平行四边形;
(2)解:在Rt△ACD中，由勾股定理得:$CD=\sqrt{AD^{2}-AC^{2}}=\sqrt{5^{2}-3^{2}}=4$,
∵点E是CD的中点，
∴CE=$\frac{1}{2}$CD=2,
∵∠ACD=90°,
∴AC⊥CE,
∴平行四边形ABCE的面积=CE·AC=2×3=6.

7. 如图,在$//ogram ABCD$中,连接对角线$BD$,点$E和点F是直线BD$上两点,且$BE= DF$.
(1)求证:四边形$AECF$是平行四边形.
(2)若$AB⊥BD$,$AB= 4$,$BC= 5$,$DE= 6$,求四边形$AECF$的面积.

答案：

(1)证明:连接AC交BD于点O,如图所示，
∵四边形ABCD是平行四边形，
∴OA=OC,OB=OD,
∵BE=DF,
∴OB+BE=OD+DF,
∴OE=OF,
∴四边形AECF是平行四边形;
(2)解:
∵四边形ABCD是平行四边形，BC=5，
∴AD=BC=5,
∵AB⊥BD,AB=4,
∴BD=$\sqrt{AD^{2}-AB^{2}}=\sqrt{5^{2}-4^{2}}=3$,
∵DE=6,DE=BD+BE,BE=DF,
∴BE=DF=3,
∴EF=BE+BD+DF=3+3+3=9,
∵四边形ABCD是平行四边形，AB⊥EF,AB=4，
∴AB//CD,AB=CD=4,CD⊥EF,
∴四边形AECF的面积为:$\frac{EF\cdot AB}{2}+\frac{EF\cdot CD}{2}=\frac{9×4}{2}+\frac{9×4}{2}=36.$