《2025年春如金卷数学暑假作业本八年级》

4. 如图,在平面直角坐标系$xOy$中,$\triangle ABC顶点的坐标分别为A(-1,0)$,$B(-2,-2)$,$C(-4,-1)$,请在图中按要求画图并解答下列问题：
(1)将$\triangle ABC$先向上平移5个单位长度,再向右平移3个单位长度,得到$\triangle A_{1}B_{1}C_{1}$($A$,$B$,$C的对应点分别为A_{1}$,$B_{1}$,$C_{1}$),画出$\triangle A_{1}B_{1}C_{1}$(要求在图上标好三角形顶点字母)；
(2)直接写出$C_{1}$的坐标______；
(3)若将$\triangle ABC绕点M顺时针旋转90^{\circ}$后,点$A$,$B$,$C的对应点分别为A_{2}(5,0)$,$B_{2}(3,1)$,$C_{2}(4,3)$,则旋转中心$M$的坐标为

______。

答案：
解：
(1)如图，$\triangle A_{1}B_{1}C_{1}$即为所求.
(2)由图可得，$C_{1}$的坐标为$(-1,4)$.
故答案为：$(-1,4)$.
(3)连接$AA_{2}$，$BB_{2}$，$CC_{2}$，分别作线段$AA_{2}$，$BB_{2}$，$CC_{2}$的垂直平分线，相交于点$M$，
则$\triangle ABC$绕点$M$顺时针旋转$90^{\circ}$后得到$\triangle A_{2}B_{2}C_{2}$，由图可得旋转中心$M$的坐标为$(2,-3)$.
故答案为：$(2,-3)$.

5. 如图,在$\triangle ABC$中,$\angle B= 45^{\circ}$。
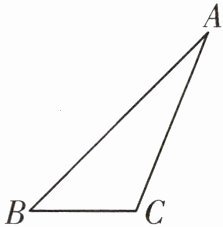
(1)用尺规作图法作$BC边上的高AD$,垂足为$D$；
(2)若$AC平分\angle BAD$,$CD= 1$,求$BC$的长。

答案：
解：
(1)如图，线段$AD$即为所求；

(2)过点$C$作$CH\perp AB$于点$H$.
$\because AC$平分$\angle BAD$，$CH\perp AB$，$CD\perp AD$，
$\therefore CH=CD=1$，
$\because\angle B=45^{\circ}$，
$\therefore BC=\sqrt{2}CH=\sqrt{2}$.

6. 如图,已知$Rt\triangle ACB$,$\angle ACB= 90^{\circ}$,请结合要求完成作图并回答相应问题：
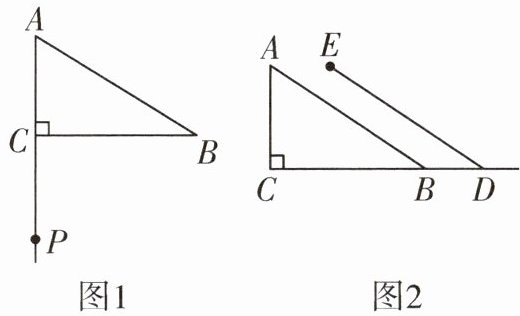
(1)如图1,点$P在线段AC的延长线上且CP= CA$,请使用不含刻度的直尺与圆规过点$P作直线PQ$,使得$PQ// AB$(不写作法,保留作图痕迹并书写相应结论)；
(2)如图2,将线段$AB水平向右进行平移m个单位长度得到线段ED$,请使用不含刻度的直尺与圆规过点$E作射线CD的垂线EF$,与$CD交于点F$(不写作法,保留作图痕迹并书写相应结论),若点$F在点B$的左侧,$CD= 12$,$FB= 5.5$,则$m= $

______。

答案：
解：
(1)如图1中，直线$PQ$即为所求；
(2)如图2中，直线$EF$即为所求.
$\because BC=DF$，
$\therefore CF=BD=\frac{1}{2}(CD-BF)=\frac{1}{2}\times(12-5.5)=\frac{13}{4}$，
$\therefore$平移的距离$m=\frac{13}{4}$.
故答案为：$\frac{13}{4}$.