第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
16. 学校准备用 2 000 元购买名著和词典,其中名著每套 70 元,词典每本 40 元,现已购买名著 20 套,最多还能买多少本词典?
答案:
解:设还能买 x 本词典,
根据题意得: $70 \times 20 + 40x \leq 2000$,
解得: $x \leq 15$,
$ \therefore x$ 的最大值为 15。
答:最多还能买 15 本词典。
根据题意得: $70 \times 20 + 40x \leq 2000$,
解得: $x \leq 15$,
$ \therefore x$ 的最大值为 15。
答:最多还能买 15 本词典。
17. 任务背景:我校在世界读书日启动“书香校园”活动,我班在参与读书活动中,计划购进一些笔记本用于摘抄“好词好句”.
驱动任务:购买笔记本的最省钱方案.
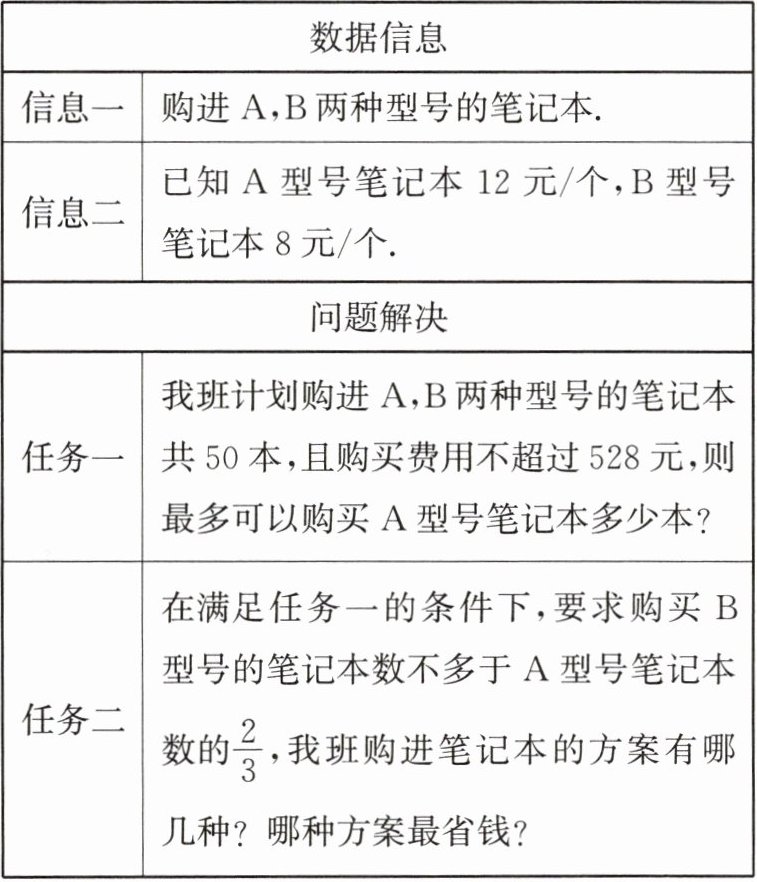
驱动任务:购买笔记本的最省钱方案.

答案:
解:任务一:设可以购买 A 型号笔记本 x 本,则可以购买 B 型号笔记本 $(50 - x)$ 本,
由题意得: $12x + 8(50 - x) \leq 528$,
解得: $x \leq 32$,
答:最多可以购买 A 型号笔记本 32 本;
任务二: $50 - x \leq \frac{2}{3}x$,
解得: $x \geq 30$,
由
(1)可知,$x \leq 32$,
$ \therefore 30 \leq x \leq 32$,
$ \because x$ 为正整数,
$ \therefore x$ 的值为 30,31,32,
$ \therefore $ 购进笔记本的方案有 3 种:
①购买 A 型号笔记本 30 本,B 型号笔记本 20 本,费用为 $12 \times 30 + 8 \times 20 = 520$ (元);
②购买 A 型号笔记本 31 本,B 型号笔记本 19 本,费用为 $12 \times 31 + 8 \times 19 = 524$ (元);
③购买 A 型号笔记本 32 本,B 型号笔记本 18 本,费用为 $12 \times 32 + 8 \times 18 = 528$ (元)。
$ \because 520 < 524 < 528$,
$ \therefore $ 购买 A 型号笔记本 30 本,B 型号笔记本 20 本,最省钱。
由题意得: $12x + 8(50 - x) \leq 528$,
解得: $x \leq 32$,
答:最多可以购买 A 型号笔记本 32 本;
任务二: $50 - x \leq \frac{2}{3}x$,
解得: $x \geq 30$,
由
(1)可知,$x \leq 32$,
$ \therefore 30 \leq x \leq 32$,
$ \because x$ 为正整数,
$ \therefore x$ 的值为 30,31,32,
$ \therefore $ 购进笔记本的方案有 3 种:
①购买 A 型号笔记本 30 本,B 型号笔记本 20 本,费用为 $12 \times 30 + 8 \times 20 = 520$ (元);
②购买 A 型号笔记本 31 本,B 型号笔记本 19 本,费用为 $12 \times 31 + 8 \times 19 = 524$ (元);
③购买 A 型号笔记本 32 本,B 型号笔记本 18 本,费用为 $12 \times 32 + 8 \times 18 = 528$ (元)。
$ \because 520 < 524 < 528$,
$ \therefore $ 购买 A 型号笔记本 30 本,B 型号笔记本 20 本,最省钱。
1. 如图是一次函数$y= kx+b$的图象,当$kx+b≥0$时,x 的取值范围是 ()
A. $x≤3$
B. $x≤0$
C. $x≤2$
D. $x≥2$
A. $x≤3$
B. $x≤0$
C. $x≤2$
D. $x≥2$
答案:
C
2. 如图,直线$y= kx+b交坐标轴于A(-3,0)$、$B(0,1)$两点,则不等式$-kx-b>0$的解集为 ()
A. $x>-3$
B. $x>3$
C. $x<-3$
D. $x<3$
A. $x>-3$
B. $x>3$
C. $x<-3$
D. $x<3$
答案:
C
3. 如图,一次函数$y_{1}= x+3与y_{2}= ax+b的图象相交于点P(1,4)$,则关于 x 的不等式$x+3≤ax+b$的解集是 ()
A. $x≥4$
B. $x≤4$
C. $x≥1$
D. $x≤1$
A. $x≥4$
B. $x≤4$
C. $x≥1$
D. $x≤1$
答案:
D
4. 如图,点$A(-1,2)在一次函数y= kx+b(k≠0)$的图象上,则不等式$kx+b>2$的解集是______.
答案:
$x < -1 $
5. 如图,一次函数$y_{1}= k_{1}x+b_{1}(k_{1}≠0)与y_{2}= k_{2}x+b_{2}(k_{2}≠0)相交于点(2,3)$,则关于 x 的不等式$k_{1}x-k_{2}x≥b_{2}-b_{1}$的解集是______.
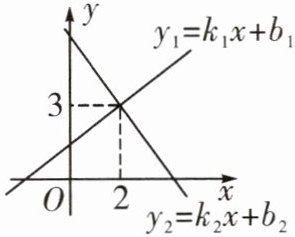

答案:
$x \geq 2 $
查看更多完整答案,请扫码查看


