《2025年春如金卷数学暑假作业本八年级》

3. 不等式$3x+1≤2x+2$的解集在数轴上表示为 ()

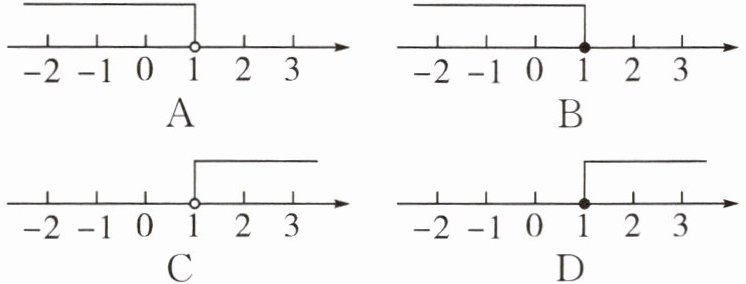
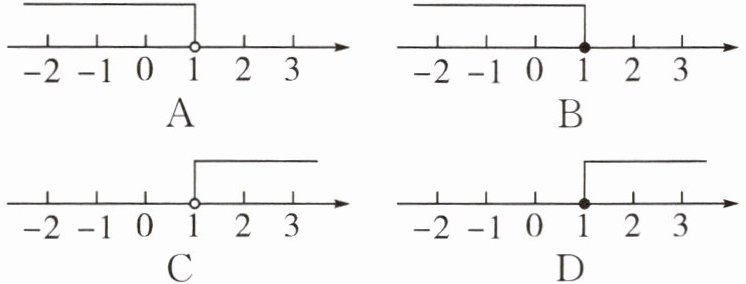
答案： B

4. 如果$(m+1)x＞m+1的解集为x＜1$,那么 m 的取值范围是 ()
A. $m＜0$
B. $m＜-1$
C. $m＞-1$
D. 为一切实数

答案： B

5. 某品牌电脑的成本价为 2 400 元,售价为 2 800 元,该商店准备举行打折促销活动,要求利润率不低于 5%,如果将这种品牌的电脑打 x 折销售,则下列不等式中能正确表示该商店的促销方式的是 ()
A. $2800x≥2400×5\%$
B. $2800x-2400≥2400×5\%$
C. $2800×\frac {x}{10}≥2400×5\%$
D. $2800×\frac {x}{10}-2400≥2400×5\%$

答案： D

6. 若$\frac {1}{2}x^{2m-1}-8＞5$是一元一次不等式,则$m= $______.

答案： 1

7. 不等式$\frac {1-x}{3}≤\frac {1-2x}{7}$的解集是______.

答案： $x \geq 4 $

8. 对于任意实数 a,b,定义一种运算$a*b= ab-a+b-2$.例如$2*5= 2×5-2+5-2= 11$.请根据上述定义解决问题:若不等式$(2*x)*3＜11$,则不等式的非负整数解为______.

答案： 0,1,2

9. 不等式$3(x+1)≥5x-3$的正整数解之和是______.

答案： 6

10. 一次环保知识竞赛共有 25 道题,规定答对一道题得 4 分,答错一题扣两分,不答则不扣分.某同学有一道题未答,如果他要想得到 80 分以上的成绩,则他至少需答对______道题目.

答案： 22

11. “618 购物节”前,天猫某品牌服装旗舰店采购了一大批服装,已知每套服装进价为 240 元,出售标价为 360 元,为了避免滞销库存,商店准备打折销售,但要保持利润不低于 20%,那么至多可打______折.

答案： 八

12. 解不等式$2x-11＜4(x-5)+3$,并把它的解集在数轴上表示出来.

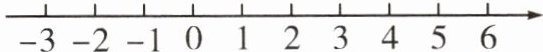
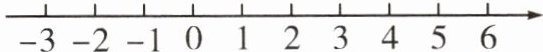
答案：
解:去括号，得 $2x - 11 ＜ 4x - 20 + 3$，
　　移项，得 $2x - 4x ＜ -20 + 3 + 11$，
　　合并同类项，得 $ -2x ＜ -6$，
　x 的系数化为 1，得 $x ＞ 3$。
　　在数轴上表示为:
　　　

13. 求不等式$3(x+1)≤4x+5$的负整数解.

答案： 解:去括号，得 $3x + 3 \leq 4x + 5$，
　　移项，得 $3x - 4x \leq 5 - 3$，
　　合并同类项，得 $ -x \leq 2$，
　　不等式的两边都除以 -1，得 $x \geq -2$。
$ \therefore $ 不等式 $3(x + 1) \leq 4x + 5$ 的负整数解为 -2,-1。

14. 解不等式$\frac {3x-1}{2}+1≥x$,并将解集在数轴上表示出来.

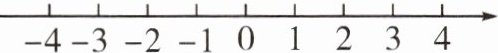
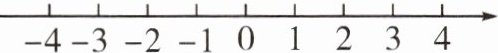
答案：
解: $ \frac{3x - 1}{2} + 1 \geq x$，
　　去分母，得 $3x - 1 + 2 \geq 2x$，
　　解得 $x \geq -1$。
　　在数轴上表示为:
　　　　

15. 已知不等式$3(x-2)-5＞6(x+1)-7的最大整数解是方程2x-mx= -10$的解,求 m 的值.

答案： 解: $3(x - 2) - 5 ＞ 6(x + 1) - 7$，
　　去括号，得 $3x - 6 - 5 ＞ 6x + 6 - 7$，
　　移项合并同类项，得 $ -3x ＞ 10$，
$ \therefore x ＜ -\frac{10}{3}$，
$ \therefore $ 最大整数解为 -4，
　　把 $x = -4$ 代入 $2x - mx = -10$，得 $ -8 + 4m = -10$，解得 $m = -\frac{1}{2}$。

6. 某班“数学兴趣小组”根据学习一次函数的经验,对函数$y= |x-2|$的图象和性质进行了研究.探究过程如下,请补充完整.
(1)自变量 x 的取值范围是全体实数.如表是 y 与 x 的几组对应值:
|x|…|-3|-2|-1|0|1|2|3|4|5|…|
|--|--|--|--|--|--|--|--|--|--|--|--|
|y|…|5|4|m|2|1|0|1|2|3|…|
其中,$m= $______;
(2)如图,在平面直角坐标系 xOy 中,描出了以表中各对对应值为坐标的点,并画出了函数图象的一部分,请画出该函数图象的另一部分;
(3)观察函数图象发现:
该函数图象的最低点坐标是______;当$x＜2$时,y 随 x 的增大而______;
(4)进一步探究:
①不等式$|x-2|≥2$的解集是______;
②若关于 x 的方程$|x-2|= kx(k≠0)$只有一个解,则 k 的取值范围是______.

答案：
解:
(1)当 $x = -1$ 时，$m = | -1 - 2 | = 3$，
　故答案为:3；
(2)利用表格中的 x,y 的对应值作为点的横纵坐标，描出各点，用平滑的线连接各点得该函数图象的另一部分如图 1:

(3)观察函数图象发现:该函数图象的最低点坐标是 $ (2,0) $，当 $x ＜ 2$ 时，y 随 x 的增大而减小，
　故答案为: $ (2,0) $，减小；
(4)①如图 2 所示:
　　　　　
　当 $y = 2$ 时，$ | x - 2 | = 2$，
　解得 $x = 0$ 或 $x = 4$，
　结合函数图象可知，当 $x \geq 4$ 或 $x \leq 0$ 时，$ | x - 2 | \geq 2$，$ \therefore | x - 2 | \geq 2$ 的解集为 $x \geq 4$ 或 $x \leq 0$，
　故答案为: $x \geq 4$ 或 $x \leq 0$；
　②观察图象，
　若关于 x 的方程 $ | x - 2 | = kx(k \neq 0)$ 只有一个解，则 k 的取值范围是 $k ＜ -1$ 或 $k \geq 1$；
　故答案为: $k ＜ -1$ 或 $k \geq 1$。