《2025年春如金卷数学暑假作业本八年级》

12. 某工厂计划生产一批吉祥物,决定选择使用 A,B 两种材料进行生产. 已知使用 B 材料的吉祥物比 A 材料每个贵 50 元,用 3000 元购买用 A 材料生产吉祥物的数量是用 1500 元购买 B 材料生产吉祥物数量的 4 倍.
(1) 求售卖一个 A 材料、一个 B 材料的吉祥物各需多少元?
(2) 一所中学为了激励学生奋发向上,准备用不超过 3000 元购买 A,B 两种材料的吉祥物共 50 个来奖励学生. 恰逢工厂对两种材料吉祥物的价格进行了调整:使用 A 材料的吉祥物的价格按售价的九折出售,使用 B 材料的吉祥物比售价提高了 20%,那么该学校此次最多可购买多少个用 B 材料的吉祥物?

答案： 解:
(1)设使用$A$材料生产的吉祥物的单价为$x$元/个,则使用$B$材料生产的吉祥物的单价为$(x + 50)$元/个,
根据题意得:$\frac{3000}{x}=\frac{1500}{x + 50}\times4$,
解得:$x = 50$,
经检验,$x = 50$是所列方程的解,且符合题意,
$\therefore x + 50=50 + 50=100$(元/个).
答:售卖一个$A$材料的吉祥物各需$50$元,售卖一个$B$材料的吉祥物需$100$元;
(2)设该学校此次购买$y$个使用$B$材料生产的吉祥物,则购买$(50 - y)$个使用$A$材料生产的吉祥物,
根据题意得:$50\times0.9(50 - y)+100\times(1 + 20\%)y\leqslant3000$,
解得:$y\leqslant10$.
答:该学校此次最多可购买$10$个使用$B$材料生产的吉祥物.

13. 【项目式学习】根据以下素材,探索完成任务.

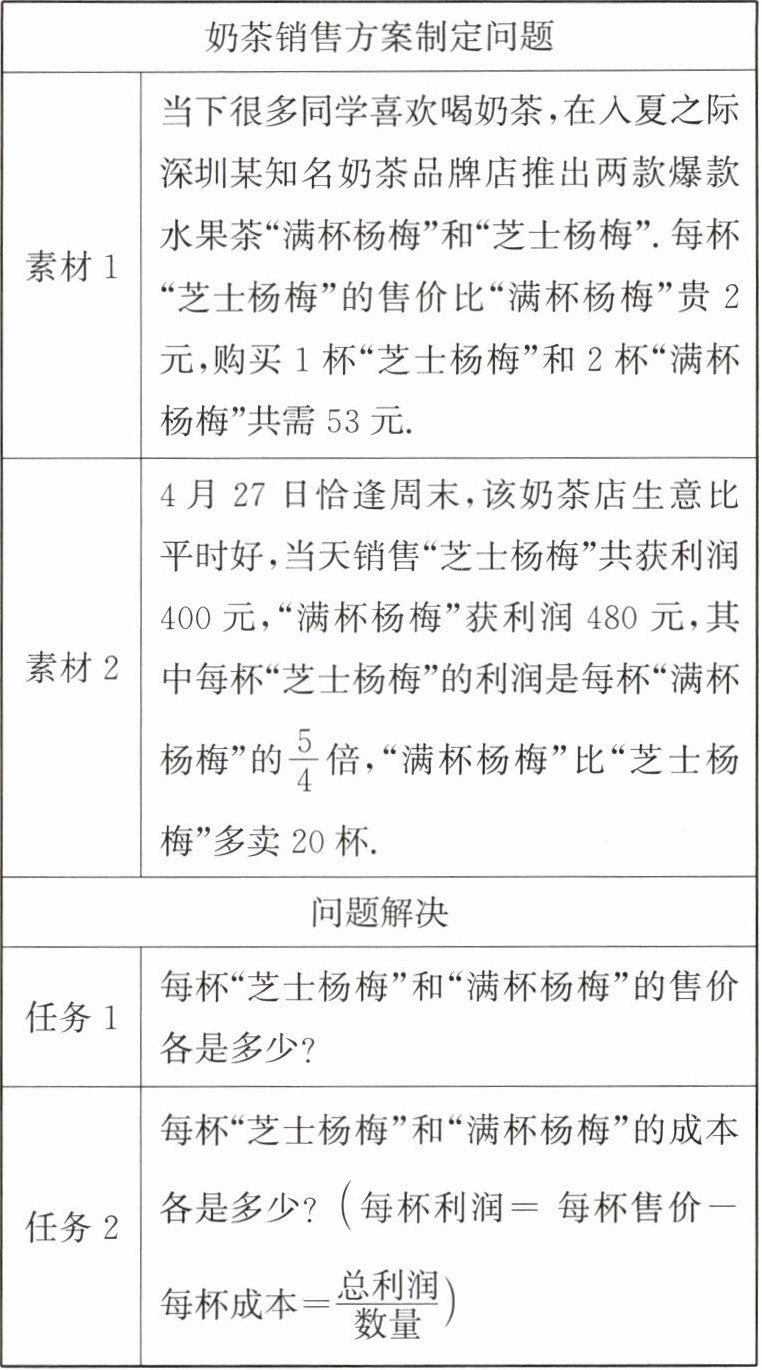
奶茶销售方案制定问题
素材 1:当下很多同学喜欢喝奶茶,在入夏之际深圳某知名奶茶品牌店推出两款爆款水果茶“满杯杨梅”和“芝士杨梅”. 每杯“芝士杨梅”的售价比“满杯杨梅”贵 2 元,购买 1 杯“芝士杨梅”和 2 杯“满杯杨梅”共需 53 元.
素材 2:4 月 27 日恰逢周末,该奶茶店生意比平时好,当天销售“芝士杨梅”共获利润 400 元,“满杯杨梅”获利润 480 元,其中每杯“芝士杨梅”的利润是每杯“满杯杨梅”的 $\frac {5}{4}$ 倍,“满杯杨梅”比“芝士杨梅”多卖 20 杯.
问题解决
任务 1:每杯“芝士杨梅”和“满杯杨梅”的售价各是多少?
任务 2:每杯“芝士杨梅”和“满杯杨梅”的成本各是多少? ( 每杯利润 = 每杯售价 - 每杯成本 $=\frac{\text{总利润}}{\text{数量}}$ )

答案： 解:任务1:
设每杯"满杯杨梅"的售价是$x$元,则每杯"芝士杨梅"的售价是$(x + 2)$元,
由题意得:$x + 2+2x=53$,
解得:$x = 17$,
$\therefore x + 2=19$,
答:每杯"满杯杨梅"的售价是$17$元,每杯"芝士杨梅"的售价是$19$元;
任务2:
设每杯"满杯杨梅"的利润是$y$元,则每杯"芝士杨梅"的利润是$\frac{5}{4}y$元,
由题意得:$\frac{480}{y}-\frac{400}{\frac{5}{4}y}=20$,
解得:$y = 8$,
经检验:$y = 8$是原方程的解,
$\therefore17 - 8=9,19 - 8\times\frac{5}{4}=9$,
答:每杯"满杯杨梅"的成本是$9$元,每杯"芝士杨梅"的成本是$9$元.