《2025年春如金卷数学暑假作业本八年级》

7. 如图,①是一个三角形,分别连接这个三角形三边中点得到图②,再连接图②中间小三角形三边的中点得到图③,按这样的方法进行下去,第$n$个图形中共有三角形的个数为

______.

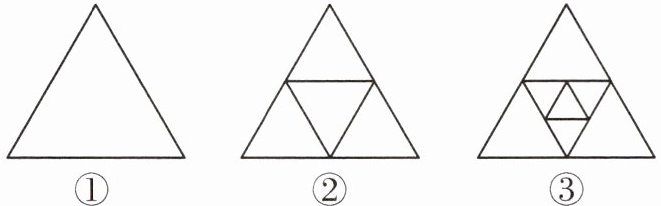
答案： 4n−3

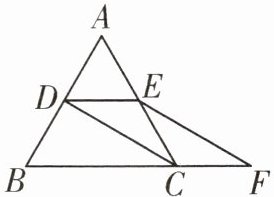
8. 如图,等边$△ABC的边长是4$,$D$,$E分别为AB$,$AC$的中点,延长$BC至点F$,使$CF= \frac{1}{2}BC$,连接$CD和EF$.
(1)求证:$DE= CF$;
(2)求四边形$DEFC$的面积.

答案：

(1)证明:
∵D,E分别为AB，AC的中点，
∴DE为△ABC的中位线，
∴DE=$\frac{1}{2}$BC,DE//BC,
又
∵CF=$\frac{1}{2}$BC,
∴DE=CF.
(2)解:由
(1)知,DE=CF=$\frac{1}{2}$BC=2,DE//CF,
∴四边形DEFC是平行四边形，
如图，过点D作DH⊥BC于H.
∵BC=AC，点D是AB的中点，
∴CD⊥AB,BD=$\frac{1}{2}$AB=2,
又
∵∠B=60°,
∴∠DCB=30°,
∴CD=$\sqrt{3}$BD=2$\sqrt{3}$,
∵∠DHC=90°,∠DCB=30°,
∴DH=$\frac{1}{2}$DC=$\sqrt{3}$,
∵DE=CF=2,
∴$S_{四边形DEFC}=CF\cdot DH=2×\sqrt{3}=2\sqrt{3}$

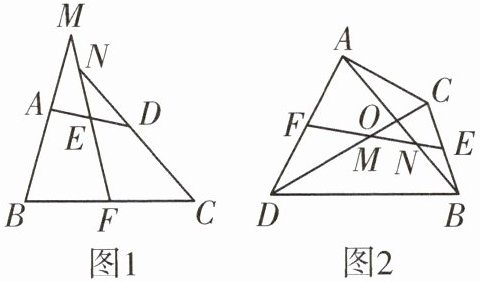
9. 如图$1$,在四边形$ABCD$中,$AB= CD$,$E$,$F分别是BC$,$AD$的中点,连接$EF$并延长,分别与$BA$,$CD的延长线交于点M$,$N$.
(1)求证:$∠BME= ∠CNE$;
(2)如图$2$,在四边形$ADBC$中,$AB与CD相交于点O$,$AB= CD$,$E$,$F分别是BC$,$AD$中点,连接$EF$,分别交$DC$,$AB于点M$,$N$,判断$△OMN$的形状.

答案：

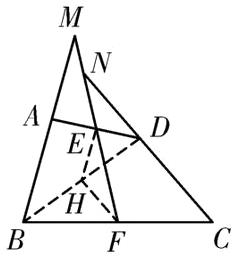
(1)证明:如图所示，连接BD，取BD的中点H，连接HE、HF，
∵E、F分别是AD、BC的中点，
∴HF、HE分别是△BCD、△ABD的中位线，
∴HF//CN,HE//BM,HF=$\frac{1}{2}$CD,HE=$\frac{1}{2}$AB,
∵AB=CD,
∴HF=HE,
∴∠HEF=∠HFE,
∵HF//CN,HE//BM,
∴∠HEF=∠BME,∠HFE=∠CNE,
∴∠BME=∠CNE;
(2)解:△OMN是等腰三角形;
证明:如图，取BD的中点H，连接HE、HF,
∵E、F分别是BC、AD的中点，
∴HF、HE分别是△ABD、△BCD的中位线，
∴HF//AB,HE//CD,HF=$\frac{1}{2}$AB,HE=$\frac{1}{2}$CD,
∵AB=CD,
∴HF=HE,
∴∠HFE=∠HEF,
∵HF//AB,HE//CD,
∴∠HFE=∠ONM,∠HEF=∠OMN,
∴∠ONM=∠OMN,
∴OM=ON,
∴△OMN是等腰三角形.

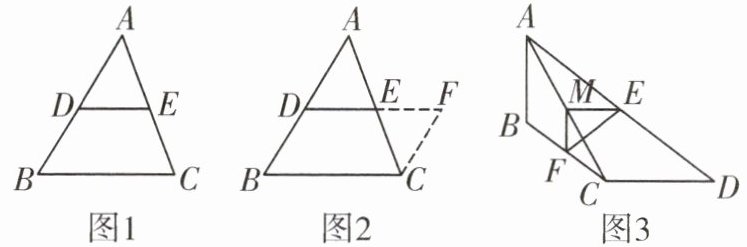
10. 【课本再现】已知:如图$1$,$DE是△ABC$的中位线. 求证:$DE// BC$,且$DE= \frac{1}{2}BC$.
(1)【定理证明】
证明:如图$2$,延长$DE至点F$,使得$EF= DE$,连接$CF$. 请你根据图$2$添加的辅助线,写出完整的证明过程;(不再添加新的辅助线)
(2)知识应用
如图$3$,在四边形$ABCD$中,$AB= 6$,$CD= 8$,$∠BAC= 30^{\circ}$,$∠ACD= 120^{\circ}$,点$E$,$F$,$M分别是AD$,$BC$,$AC$的中点,求$EF$的长.

答案：
(1)证明:在△AED和△CEF中，
$\begin{cases}DE = FE \\ ∠AED = ∠CEF \\ AE = CE\end{cases}$
∴△AED≌△CEF(SAS),
∴AD=CF,∠A=∠ECF,
∴AB//CF,
∵AD=BD,
∴BD=CF,
∴四边形DBCF为平行四边形，
∴DF//BC,DF=BC,
∴DE//BC,DE=$\frac{1}{2}$BC;
(2)解:
∵点E,M分别是AD，AC的中点，
∴EM是△ADC的中位线，
∴EM=$\frac{1}{2}$CD=4,EM//CD,
∴∠EMC+∠ACD=180°,
∵∠ACD=120°,
∴∠EMC=60°,
同理可得:MF=$\frac{1}{2}$AB=3,MF//AB,
∴∠CMF=∠BAC,
∵∠BAC=30°,
∴∠CMF=30°,
∴∠EMF=90°,
∴EF=$\sqrt{EM^{2}+MF^{2}}=\sqrt{4^{2}+3^{2}}=5.$