《2025年春如金卷数学暑假作业本八年级》

7. 如图,一束太阳光线平行照射在放置于地面的等边$\triangle ABC$上,若$\angle 1= 24^{\circ}$,则$\angle 2$的度数为()
A. $24^{\circ}$
B. $36^{\circ}$
C. $48^{\circ}$
D. $56^{\circ}$

答案： B

8. 如图,为了让电线杆垂直于地面,工程人员的操作方法通常是:从电线杆$DE上一点A往地面拉两条长度相等的固定绳AB与AC$,当固定点$B$,$C到杆脚E$的距离相等,且点$B$,$E$,$C$在同一直线上时,电线杆$DE\perp BC$.工程人员的这种操作方法的依据是()
A. 等角对等边
B. 等腰三角形三线合一的性质
C. 两点之间线段最短
D. 垂线段最短

答案： B

9. 如图,是屋顶的剖面图,屋檐$AB= AC= 5\ \text{m}$,横梁$BC= 8\ \text{m}$,在横梁$BC上的某一点D处要支一根木头连接屋顶A$,则这根木头的长度可能是()
A. $2.5\ \text{m}$
B. $6\ \text{m}$
C. $4\ \text{m}$
D. $8\ \text{m}$

答案： C

10. 如图,在格点中找一点$C$,使得$\triangle ABC$是等腰三角形,且$AB$为其中的一条腰,则这样的点$C$一共有()
A. $3$个
B. $4$个
C. $5$个
D. $6$个

答案： C

11. 已知等腰三角形的周长为$20\ \text{cm}$,一边长为$6\ \text{cm}$,则底边长为______$\text{cm}$.

答案： 6或8

12. 已知$\triangle ABC$为等边三角形,$BD为\triangle ABC$的高,延长$BC至E$,使$CE= CD= 1$,连接$DE$,则$BE= $______.

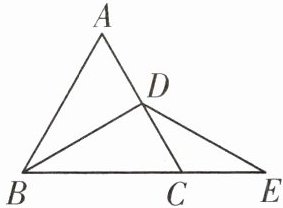
答案： 3

13. “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒$PB$,$PD$组成,两根棒在$P点相连并可绕P$转动,$C$点固定,$CP= OC= OA$,点$O$,$A$可在槽中滑动,若$\angle AOB= 75^{\circ}$,则$\angle P$的度数是______.

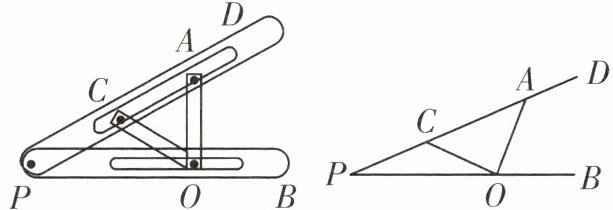
答案： 25°

14. 如图,在等边$\triangle ABC$中,$AB= 3$,$\angle ABC和\angle ACB的平分线相交于点O$,过$O作OE// AB$,$OF// AC$,交$BC于点E$,$F$,则$\triangle OEF$的周长为______.

答案： 3

15. 如图,$\triangle ABC$是等边三角形,$DE// BC$,分别交$AB$,$AC于点D$,$E$.求证:$\triangle ADE$是等边三角形.以下为淇淇同学的证明方法,请补全:
证明:$\because\triangle ABC$是等边三角形,
$\therefore\angle B= \angle C$,$\angle A= 60^{\circ}$,
$\because DE// BC$,
$\therefore\angle B= \angle ADE$,$\angle C= $①______,
$\therefore\angle ADE= $②______,
$\therefore$③______$=AE$.
$\therefore\triangle ADE$是等腰三角形.
又$\angle A= 60^{\circ}$,
$\therefore\triangle ADE$是等边三角形.(④______)

答案： ∠AED;∠AED;AD;有一个内角是60°的等腰三角形是等边三角形.