《2025年春如金卷数学暑假作业本八年级》

9. 【问题发现】我们知道“线段垂直平分线上的点到线段两端的距离相等”,那么不在线段垂直平分线上的点到线段两端的距离大小如何判断呢?
【自主研究】
(1)如图$1$,直线$l是线段AB$的垂直平分线,点$P在直线l$的左侧,经测量,$PA＜PB$,请证明这个结论;
【迁移研究】
(2)如图$2$,直线$l是线段AB$的垂直平分线,点$C在直线l$外,且与点$A在直线l$的同侧,点$D是直线l$上的任意一点,连接$AD$,$BC$,$CD$,试判断$BC和AD+CD$之间的大小关系,并说明理由.

答案：

(1)证明:如图1,连接PA,PB,AM,
　　　　　　　　　　　　　　　　　
　
∵直线l是线段AB的垂直平分线，
　
∴AM=BM,
　
∴PB=PM+MB=PM+AM,
　
∵PM+AM＞PA,
　
∴PA＜PB;
(2)解:如图2,AD+CD≥BC,理由如下:
　　当D不在线段BC上时，
　　连接BD,
　
∵直线l是线段AB的垂直平分线，
　
∴AD=BD,
　
∵BD+CD＞BC,
　
∴AD+CD＞BC,
　　当D在线段BC上时，AD+CD=BC，
　　　　　　　　　　　　　　　　　
　
∴AD+CD≥BC.

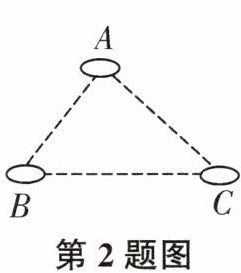
1. 如图,为了促进当地旅游发展,某地要在三条公路围城的一块三角形平地$ABC$上修建一个度假村.要使这个度假村到三条公路的距离相等,应该修在()


A. $\triangle ABC$三边中线的交点处
B. $\triangle ABC$三个角的平分线的交点处
C. $\triangle ABC$三边高线的交点处
D. $\triangle ABC$三边垂直平分线的交点处

答案： B

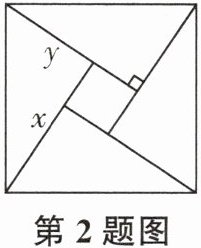
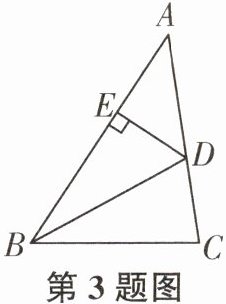
2. 如图,在$\text{Rt}\triangle ABC$中,$\angle ACB= 90^{\circ}$,根据尺规作图的痕迹,下列结论不一定正确的是()



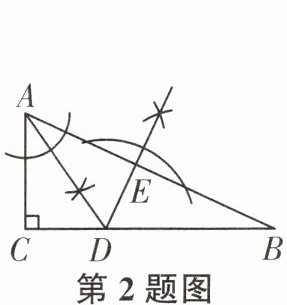
A. $DE\perp AB$
B. $AD= BD$
C. $DE= DC$
D. $\angle BDE= \angle BAC$

答案： B

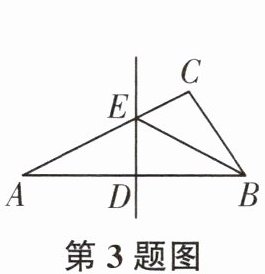
3. 如图,$BD是\triangle ABC$的角平分线,$DE\perp AB于点E$,$\triangle ABC的面积为8$,$AB= 5$,$DE= 2$,则$BC$的长为()



A. $3$
B. $4$
C. $5$
D. $7$

答案： A

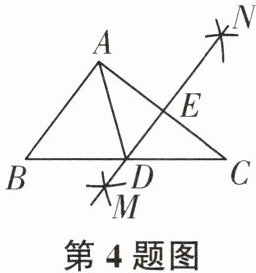
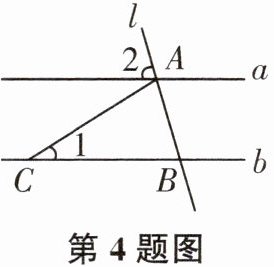
4. 如图,在$\triangle ABC$中,$\angle ABC$,$\angle EAC的平分线BP$,$AP交于点P$,延长$BA$,$BC$,$PM\perp BE$,$PN\perp BF$,则下列结论中正确的有()
①$CP平分\angle ACF$;②$\angle ABC+2\angle APC= 180^{\circ}$;③$\angle ACB= 2\angle APB$;④$S_{\triangle PAC}= S_{\triangle MAP}+S_{\triangle NCP}$.



A. $1$个
B. $2$个
C. $3$个
D. $4$个

答案： D

5. 如图,在$\text{Rt}\triangle ABC$中,$\angle C= 90^{\circ}$,以$A$为圆心,任意长为半径画弧,分别交$AC$,$AB于点M$,$N$,再分别以$M$,$N$为圆心,大于$\frac{1}{2}MN$的长为半径画弧,两弧交于点$O$,作射线$AO交BC于点D$,若$CD= 2$,$P为AB$上一动点,则$PD$的最小值为______.

答案： 2