《2025年一本预备新高一物理》

【变式】在某城市的一条道路上,规定车辆行驶速度不得超过 30 km/h。在一次交通事故中,肇事车是一辆客车,测得这辆车沿直线紧急刹车(车轮被抱死)时留下的刹车痕迹长为 7.6 m,已知该客车刹车时的加速度大小为 $ 7 m/s^2 $。请判断该车是否超速。

答案： 解：由公式 $ v^2 - v_0^2 = 2ax $ 得，$ v = 0 $ 时，$ v_0^2 = -2ax $，已知车辆的最大行驶速度为 $ 30 \, \text{km/h} \approx 8.3 \, \text{m/s} $
车辆在不超速的情况下紧急刹车的最大位移 $ x = \frac{v_0^2}{-2a} \approx 5.0 \, \text{m} ＜ 7.6 \, \text{m} $，而本题中客车沿直线刹车痕迹为 7.6 m，说明该客车刹车时速度大于 30 km/h，即该车超速。

1.(教材改编题)2024 年 11 月 4 日,神舟十八号载人飞船返回舱在东风着陆场成功着陆。神舟十八号载人飞船返回舱在离地面 1 m 时,点燃反推燃料,产生巨大的反推力来缓冲降落,使返回舱到达地面时的速度为零。若返回舱下落最后 1 m 的过程可视为做加速度大小为 $ 32 m/s^2 $ 的匀减速直线运动,则返回舱距地面 1 m 时的速度大小为 (D)
A. 20 m/s
B. 16 m/s
C. $ 4\sqrt{5} m/s $
D. 8 m/s

答案： D 由运动学公式 $ v^2 = 2ah $ 可得，返回舱距地面 1 m 时的速度大小为 $ v = \sqrt{2ah} = \sqrt{2 \times 32 \times 1} \, \text{m/s} = 8 \, \text{m/s} $，故 D 正确。

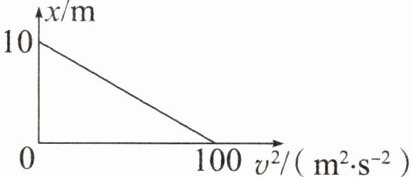
2. 一辆遥控汽车在平直的轨道上匀速运动,为了测试其刹车性能,从 $ t = 0 $ 起开始刹车,刹车过程中遥控汽车的位移与速度平方的关系如图所示。下列说法正确的是 (B)

A. 遥控汽车刹车时产生的加速度大小为 $ 10 m/s^2 $
B. 遥控汽车从刹车到停止运动所需时间为 2 s
C. 遥控汽车在刹车后第 1 s 内的位移大小为 2.5 m
D. 遥控汽车刹车后 1 s 末的速度大小为 10 m/s

答案： B 由题图可知，当遥控汽车位移为 0 时，速度的平方为 $ 100 \, \text{m}^2/\text{s}^2 $，即遥控汽车的初速度为 10 m/s，刹车总位移是 10 m，根据 $ 0 - v_0^2 = 2ax $ 解得 $ a = -\frac{v_0^2}{2x} = -5 \, \text{m/s}^2 $，故 A 错误；遥控汽车从刹车到停止运动所需时间为 $ t = \frac{0 - v_0}{a} = 2 \, \text{s} $，故 B 正确；遥控汽车在刹车后第 1 s 内的位移大小为 $ x = v_0t_1 + \frac{1}{2}at_1^2 = 7.5 \, \text{m} $，故 C 错误；遥控汽车刹车后 1 s 末的速度大小为 $ v_1 = v_0 + at_1 = 5 \, \text{m/s} $，故 D 错误。

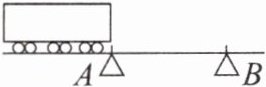
3. 如图所示,一列长为 $ L $ 的火车沿平直轨道匀加速驶过长为 $ L $ 的水平桥,车头通过桥头 $ A $ 时的速度是 $ v_1 $,车头通过桥尾 $ B $ 时的速度是 $ v_2 $,则车尾通过桥尾时的速度为 (D)


A. $ v^2 $
B. $ 2v_2 - v_1 $
C. $ \sqrt{\frac{v_2^2 + v_1^2}{2}} $
D. $ \sqrt{2v_2^2 - v_1^2} $

答案： D 火车车头从桥头到桥尾运动的过程中，由速度与位移关系式得 $ v_2^2 - v_1^2 = 2aL $，从火车车头通过桥头到火车车尾通过桥尾的过程中，有 $ v^2 - v_1^2 = 2a \cdot 2L $，解得 $ v = \sqrt{2v_2^2 - v_1^2} $，故 D 正确。