第116页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
3. 关于弹簧的劲度系数,下列说法正确的是(
A. 与弹簧受的拉力有关
B. 与弹簧发生的形变有关
C. 由弹簧本身决定,与弹簧所受的拉力大小及形变程度无关
D. 与弹簧本身特征、所受拉力大小、形变的大小都有关
C
)A. 与弹簧受的拉力有关
B. 与弹簧发生的形变有关
C. 由弹簧本身决定,与弹簧所受的拉力大小及形变程度无关
D. 与弹簧本身特征、所受拉力大小、形变的大小都有关
答案:
弹簧的劲度系数反映弹簧的软硬程度,它的数值与弹簧的材料,弹簧丝的粗细,弹簧圈的直径,单位长度的匝数及弹簧的原长有关,与弹簧所受拉力及形变量大小无关,故C正确,A、B、D错误。
4. 下列各图中,接触面都是光滑的,且物体均保持静止。则$Q$球只受一个弹力的有(
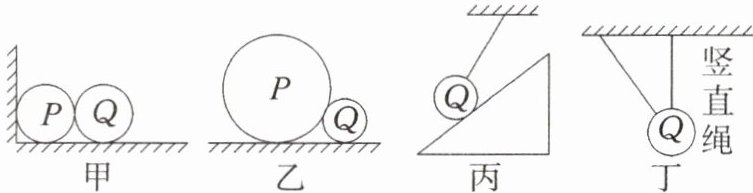
A. 甲、乙
B. 甲、乙、丙
C. 甲、乙、丁
D. 甲、乙、丙、丁
C
)
A. 甲、乙
B. 甲、乙、丙
C. 甲、乙、丁
D. 甲、乙、丙、丁
答案:
甲图中地面对Q有向上的弹力,假设两球间有弹力则小球Q将向右运动,可知P、Q间无弹力,即Q只受一个弹力;乙图地面对Q有向上的弹力,假设两球间有弹力则两球将向两边运动,可知PQ间无弹力,即Q只受一个弹力;丙图中Q受细绳的拉力和斜面的支持力两个弹力作用;丁图中因上面的细绳竖直,可知旁边的细绳无弹力,否则中间细绳不会竖直,即Q只受一个弹力。故选C。
5. 如图所示,一根弹性杆的一端固定在倾角为$30^{\circ}$的斜面上,杆的另一端固定一个重$2 N$的小球,小球处于静止状态,则弹性杆对小球的弹力(

A. 大小为$2 N$,方向平行于斜面向上
B. 大小为$2 N$,方向垂直于斜面向上
C. 大小为$2 N$,方向竖直向上
D. 大小为$1 N$,方向沿杆的切线方向
C
)
A. 大小为$2 N$,方向平行于斜面向上
B. 大小为$2 N$,方向垂直于斜面向上
C. 大小为$2 N$,方向竖直向上
D. 大小为$1 N$,方向沿杆的切线方向
答案:
要注意活动杆的弹力一定沿着杆,而固定杆的弹力可以沿任意方向。对小球进行受力分析,小球受到重力G和弹性杆对小球的弹力F,由于小球处于静止状态,弹力与重力平衡,则弹性杆对小球的弹力方向应竖直向上,大小为$F = G = 2N$,故A、B、D错误,C正确。
6. 如图所示的装置中,小球的质量均相同,弹簧和细线的质量均不计,一切摩擦忽略不计,平衡时各弹簧的弹力分别为$F_{1}$、$F_{2}$、$F_{3}$,其大小关系是(
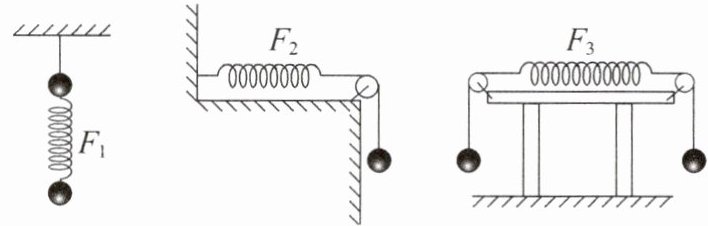
A. $F_{1} = F_{2} = F_{3}$
B. $F_{1} = F_{2} < F_{3}$
C. $F_{1} = F_{2} > F_{3}$
D. $F_{1} > F_{2} > F_{3}$
A
)
A. $F_{1} = F_{2} = F_{3}$
B. $F_{1} = F_{2} < F_{3}$
C. $F_{1} = F_{2} > F_{3}$
D. $F_{1} > F_{2} > F_{3}$
答案:
根据二力平衡,弹簧弹力均等于一个小球的重力,所以有$F_1 = F_2 = F_3$,故A正确。
7. 如图甲所示,用铁架台、弹簧和多个已知质量且质量相等的钩码,探究“在弹性限度内弹簧弹力与弹簧伸长量的关系”实验。

(1) 该实验用钩码所受的重力等于弹簧受到的弹力理由是
(2) 如图乙所示,根据实验数据绘图,纵轴是钩码质量$m$,横轴是弹簧的形变量$x$。由图像可得结论:在弹簧的弹性限度内,弹簧的弹力与弹簧的伸长量成

(1) 该实验用钩码所受的重力等于弹簧受到的弹力理由是
当钩码处于静止状态时,根据二力平衡可知,钩码所受的重力等于弹簧对钩码的弹力,而弹簧对钩码的弹力与弹簧受到的弹力是一对相互作用力,大小相等
。(2) 如图乙所示,根据实验数据绘图,纵轴是钩码质量$m$,横轴是弹簧的形变量$x$。由图像可得结论:在弹簧的弹性限度内,弹簧的弹力与弹簧的伸长量成
正比
(选填“正比”或“反比”),弹簧的劲度系数$k = $5
$N/m$(重力加速度$g取10 m/s^{2}$)。
答案:
【答案】(1)见解析 (2)正比 5
【解析】(1)当钩码处于静止状态时,根据二力平衡可知,钩码所受的重力等于弹簧对钩码的弹力。
(2)由图像乙知,所挂钩码质量m与弹簧形变量x成正比,所以钩码所受的重力mg与弹簧形变量x也成正比,由于所挂钩码重力mg等于弹簧受到的弹力F,所以可得出结论:在弹簧的弹性限度内,弹簧的弹力与弹簧的伸长量成正比;根据胡克定律$F = kx$,可得弹簧的劲度系数$k = \frac{\Delta F}{\Delta x} = \frac{\Delta mg}{\Delta x} = \frac{40×10×10^{-3}}{8×10^{-2}}N/m = 5N/m$。
【解析】(1)当钩码处于静止状态时,根据二力平衡可知,钩码所受的重力等于弹簧对钩码的弹力。
(2)由图像乙知,所挂钩码质量m与弹簧形变量x成正比,所以钩码所受的重力mg与弹簧形变量x也成正比,由于所挂钩码重力mg等于弹簧受到的弹力F,所以可得出结论:在弹簧的弹性限度内,弹簧的弹力与弹簧的伸长量成正比;根据胡克定律$F = kx$,可得弹簧的劲度系数$k = \frac{\Delta F}{\Delta x} = \frac{\Delta mg}{\Delta x} = \frac{40×10×10^{-3}}{8×10^{-2}}N/m = 5N/m$。
查看更多完整答案,请扫码查看


