《2025年一本预备新高一物理》

7.测定当地的重力加速度的装置如图甲所示,该实验要在暗室中进行,实验器材包括:频闪仪(带照相功能)、尖嘴玻璃管、螺丝夹子、接水铝盒、带荧光刻度的刻度尺、支架、漏斗、橡胶管等。

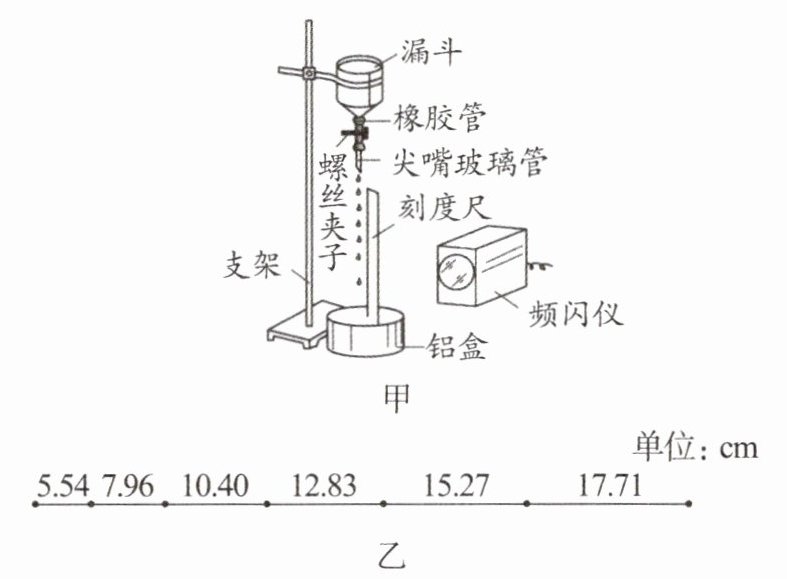
实验步骤如下:
(1)在漏斗内盛满水,旋松螺丝夹子,使水滴以一定的频率一滴滴落下;
(2)用频闪仪发出的闪光将水滴照亮,由大到小逐渐调节频闪仪的闪光频率,直到频闪仪的闪光频率为10Hz时,第一次看到一串仿佛固定不动的水滴,此时水滴滴落的频率为10Hz;
(3)调节螺丝夹子,加快水滴滴落的频率,再用该频闪仪发出的闪光将水滴照亮,直到第二次看到一串仿佛固定不动的水滴;
(4)利用频闪仪拍照;
(5)用竖直放置的米尺测得各水滴所对应的刻度。采集数据并处理,若测出其中几个连续的水滴的距离关系如图乙所示(圆点代表水滴),当地的重力加速度大小$g= $9.7m/s^2;(结果保留两位有效数字)
(6)该实验中测得的重力加速度总是偏小的原因可能是存在空气阻力。(写出一条即可)

答案： 【答案】
(2)10
(5)9.7
(6)存在空气阻力
【解析】
(2)当频闪仪闪光频率等于水滴滴落的频率时，可看到一串仿佛固定不动的水滴，可知水滴滴落的频率为10Hz。
(5)设滴水的时间间隔为$T_{0}$，频闪仪的拍照周期为$T = 0.1s$，$T_{0}=\frac{T}{n}(n = 2,3,4,\cdots)$，由运动学规律可知$g=\frac{(x_{4}+x_{5}+x_{6})-(x_{1}+x_{2}+x_{3})}{(3T_{0})^{2}}$，代入数据联立，当$n = 2$时，解得$g\approx9.7m/s^{2}$。
(6)存在空气阻力，水滴没有做自由落体运动。
【特别提醒】因为第一次看到一串仿佛固定不动的水滴时，频闪频率和水滴下落频率相等，为10Hz，对应相邻水滴间的时间间隔为$T = 0.1s$。再调快水滴下落的频率，当再次看到一串仿佛固定不动的水滴时，水滴下落的频率正好是第一次的整数倍，即相邻水滴间的时间间隔$T_{0}=\frac{T}{n}(n = 2,3,4,\cdots)$。

8.如图所示,一滴雨滴从离地面20m高的楼房屋檐自由下落,下落5m时,刚好到达窗口上沿,再经$\Delta t = 0.2$s的时间通过窗口,$g$取10m/s^2,求:

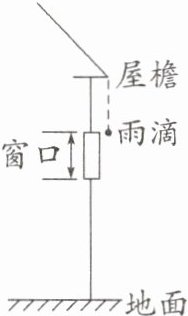
(1)雨滴落地前瞬间的速度大小为20m/s;
(2)窗口上下沿的高度差为2.2m。

答案： 解：
(1)由公式$h=\frac{1}{2}gt^{2}$得，雨滴下落的时间$t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2\times20}{10}}s = 2s$落地速度为$v = gt = 10\times2m/s = 20m/s$
(2)雨滴下落到窗口上沿的时间$t_{1}=\sqrt{\frac{2h_{1}}{g}}=\sqrt{\frac{2\times5}{10}}s = 1s$，下落到窗口下沿的时间$t_{2}=t_{1}+\Delta t = 1s + 0.2s = 1.2s$楼房屋檐到窗口下沿的高度$h_{2}=\frac{1}{2}gt_{2}^{2}=\frac{1}{2}\times10\times1.2^{2}m = 7.2m$窗口上下沿的高度差$\Delta h = h_{2}-h_{1}=7.2m - 5m = 2.2m$。