第86页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
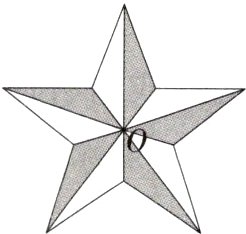
7.(2024湖南怀化中方期末,4,★☆☆)如图,把图中的五角星图案,绕着它的中心O旋转,旋转角至少为______度时,旋转后的五角星能与自身重合.(M7205003) ( )
A. 60
B. 30
C. 72
D. 36

A. 60
B. 30
C. 72
D. 36
答案:
∵360°÷5 = 72°,
∴旋转72°的整数倍,就可以与自身重合,
∴旋转角至少为72°.故选C.
∵360°÷5 = 72°,
∴旋转72°的整数倍,就可以与自身重合,
∴旋转角至少为72°.故选C.
8. 新考法 (2022四川广安岳池期中,23,★★☆)如图①所示,在4×4的方格内,已将其中的4个小正方形涂成灰色,请你分别在图②、图③、图④、图⑤中再将两个空白的小正方形涂成灰色,使4个灰色小正方形组成一个轴对称图形,画出与图①不同的4种方案.(每个4×4的方格内限画一种,若两个方案的图形经过翻折、平移、旋转后能够重合,则视为一种方案)
要求:(1)4个灰色小正方形必须相连;(有公共顶点视为相连)
(2)将选中的小正方形方格用铅笔涂成灰色图形.


要求:(1)4个灰色小正方形必须相连;(有公共顶点视为相连)
(2)将选中的小正方形方格用铅笔涂成灰色图形.


答案:
解析 本题主要考查网格中的作图问题.
如图所示(答案不唯一).




解析 本题主要考查网格中的作图问题.
如图所示(答案不唯一).




9.(几何直观)阅读下列材料,完成相应的学习任务.
旋转对称
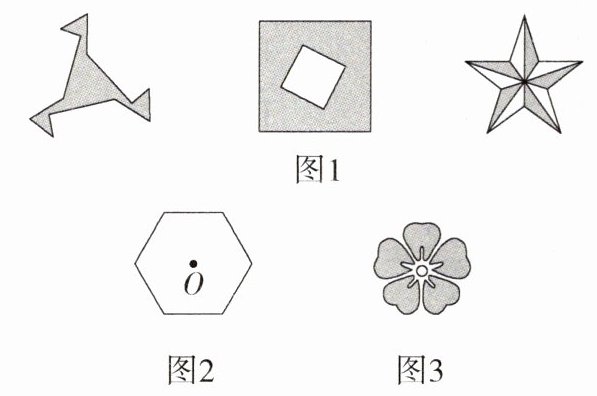
把正n边形绕着它的中心旋转$\frac{360}{n}$的整数倍后,所得的图形与原正n边形重合,我们说正n边形关于其中心有$\frac{360}{n}$的旋转对称. 一般地,如果一个图形绕着某点O旋转α(0<α<360°)后,所得到的图形与原图形重合,则称此图形关于点O有α的旋转对称. 图1中的三个图形就具有旋转对称性质.
任务:(M7205003)
(1)如图2,正六边形关于其中心O有______的旋转对称.
(2)图3是利用旋转变换设计的具有旋转对称性质的一个图形,将该图形绕其中心至少旋转______与原图形重合.
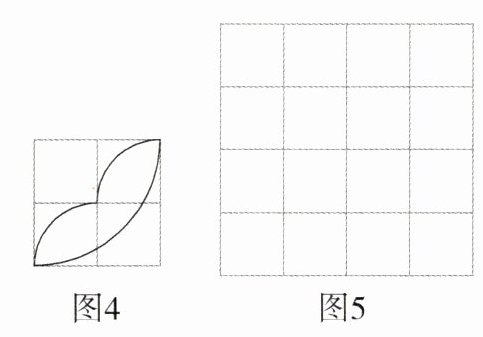
(3)请以图4为基本图案,在图5中利用平移、轴对称或旋转进行图案设计,使得设计出的图案绕其中一个点旋转180°后与自身重合.
旋转对称
把正n边形绕着它的中心旋转$\frac{360}{n}$的整数倍后,所得的图形与原正n边形重合,我们说正n边形关于其中心有$\frac{360}{n}$的旋转对称. 一般地,如果一个图形绕着某点O旋转α(0<α<360°)后,所得到的图形与原图形重合,则称此图形关于点O有α的旋转对称. 图1中的三个图形就具有旋转对称性质.


任务:(M7205003)
(1)如图2,正六边形关于其中心O有______的旋转对称.
(2)图3是利用旋转变换设计的具有旋转对称性质的一个图形,将该图形绕其中心至少旋转______与原图形重合.
(3)请以图4为基本图案,在图5中利用平移、轴对称或旋转进行图案设计,使得设计出的图案绕其中一个点旋转180°后与自身重合.
答案:
解析
(1)60%.
(2)72°.
(3)如图所示(答案不唯一).

解析
(1)60%.
(2)72°.
(3)如图所示(答案不唯一).

查看更多完整答案,请扫码查看


