《2025年5年中考3年模拟七年级数学下册湘教版》

1.（2024湖南郴州嘉禾月考）如图，如果∠1 = ∠2，那么AB//CD，其依据可以简单说成（ ）
A.两直线平行，内错角相等
B.内错角相等，两直线平行
C.两直线平行，同位角相等
D.同位角相等，两直线平行
　　　 

答案： D
∵∠1 = ∠2,
∴AB//CD(同位角相等,两直线平行),故选D.

2.如图，∠1 = 120°，要使a//b，则∠2的度数是（M7204005）（ ）
A.60°
B.80°
C.100°
D.120°

答案： 如果∠2 = ∠1 = 120°,那么a//b,所以要使a//b,则∠2的度数是120°.故选D.

3.（2024广西柳州期末）如图所示，用直尺和三角尺作直线AB，CD，由图可知，直线AB与直线CD的位置关系为________.（M7204005）

答案： 答案 平行
解析 根据题意,∠DEF与∠BHF是三角尺的同一个角,所以∠DEF = ∠BHF,所以AB//CD(同位角相等,两直线平行).

4.教材变式 如图所示的是由四条射线构成的“鱼”形图案，已知∠1 = 40°，∠2 = 40°，∠4 = 140°，求∠3的度数.

答案： 解析
∵∠1 = 40°,∠2 = 40°,
∴∠1 = ∠2,
∴AB//DC,
∴∠4+∠3 = 180°,
又∠4 = 140°,
∴∠3 = 180° - 140° = 40°.

5.（2024湖南湘西州凤凰月考，5，★）如图，已知∠B = ∠AEF，则（M7204005）（ ）

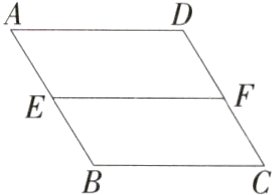
A.EF//BC
B.AD//EF
C.AD//BC
D.AB//CD

答案： A
∵∠B = ∠AEF,
∴EF//BC,故选项A正确,无法判断AD//EF、AD//BC、AB//CD是否成立.故选A.

6.（2024湖南师大附中月考，20，）如图，点D在BC上，DE、AB交于点F，AE//BC，∠BFD = ∠BAC.试说明：∠E = ∠C.（M7204005）
　

答案： 证明
∵AE//BC,
∴∠E = ∠BDF,
∵∠BFD = ∠BAC,
∴AC//DE,
∴∠C = ∠BDF,
∴∠E = ∠C.

7.几何直观 如图，M、F两点在直线CD上，AB//CD，CB//DE，BM、DN分别平分∠ABC、∠EDF.试说明：BM//DN.（M7204005）
　　　　　　　　　　　　　　　　　

答案： 证明
∵AB//CD,
∴∠ABC = ∠BCD,∠ABM = ∠BMC,
∵BC//ED,
∴∠EDF = ∠BCD,
∴∠ABC = ∠EDF,
∵BM、DN分别平分∠ABC、∠EDF,
∴∠ABM = $\frac{1}{2}$∠ABC,∠NDF = $\frac{1}{2}$∠EDF,
∴∠BMC = ∠ABM = ∠NDF,
∴BM//DN.