《2025年5年中考3年模拟七年级数学下册湘教版》

9.(2024广东深圳盐田期末)利用如图所示的方法，可以折出“过已知直线外一点P且与已知直线AB平行”的直线.下列解释正确的是(M7204005)
　(　　)
　　
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.以上解释都正确

答案：
D如图,

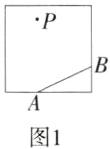
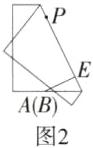
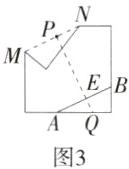
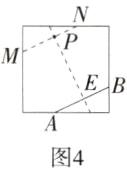
由图2的操作可知PE⊥AE,所以∠PEA=90°,由图3 的操作可知MN⊥PE,所以∠MPE=∠NPE=90°,所以∠MPE=∠NPE=∠AEP=∠BEP=∠AEQ=∠BEQ=90°,所以可依据同位角相等，两直线平行或内错角相等，两直线平行或同旁内角互补，两直线平行判定AB//MN,故选D.

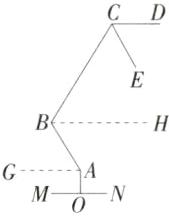
10.如图所示的是一盏可调节台灯(如图1)及其示意图(如图2).固定支撑杆AO垂直于底座MN于点O,AB与BC是分别可绕点A和B旋转的调节杆,台灯灯罩可绕点C旋转调节光线角度,在调节过程中,最外侧光线CD、CE组成的∠DCE始终保持不变.现调节台灯,使外侧光线CD//MN,CE//BA,若∠BAO = 158°,则∠DCE =(M7204004)　(　　)
　　　　 　
A.58°　　
B.68°　　
C.32°　　
D.22°

答案：
B　如图所示,过点A作AG//MN,过点B作BH//CD,

∵CD//MN,
∴AG//MN//BH//CD,
∵OA⊥MN,
∴AG⊥OA,即∠OAG=90°,
∵∠BAO=158°,
∴∠BAG=∠BAO−∠OAG=68°,
∴∠ABH=∠BAG=68°,
∵CE//AB,BH//CD,
∴∠ABC+∠BCE=180°=∠CBH+∠BCD,
∴∠ABH+∠CBH+∠BCE=180°=∠CBH+∠BCE+∠DCE,
∴∠DCE=∠ABH=68°,故选B.

11.(2024广西中考)已知∠1与∠2为对顶角，∠1 = 35°，则∠2 = ________.(M7204002)

答案： 答案　35°
解析
∵∠1与∠2为对顶角,∠1=35°,
∴∠2=∠1=35°.故答案为35°.

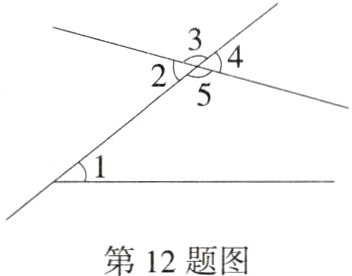
12.(三线八角模型)如图,与∠1是同旁内角的是________.(M7204002)
　

答案： 答案　∠5
解析　根据“两条直线被第三条直线所截，位于这两条直线的内部且在截线同侧，这样的两个角叫作同旁内角”进行判断即可.

13.(2024湖南株洲炎陵期中)如图,已知AC⊥BC,CD⊥AB,那么点A到CD的距离是线段________的长.(M7204006　

答案： 答案　AD
解析
∵CD⊥AB,
∴点A到CD的距离是线段AD 的长.

14.如图,∠ABC = 90°,AB = 10cm,∠D + ∠C = 180°,则AD与BC之间的距离是________.(M7204007)
　

答案： 答案　10cm
解析
∵∠D+∠C=180°,
∴AD//BC,
∵∠ABC=90°,
∴AB的长即为AD与BC之间的距离，
∵AB=10cm,
∴AD与BC之间的距离是10cm.

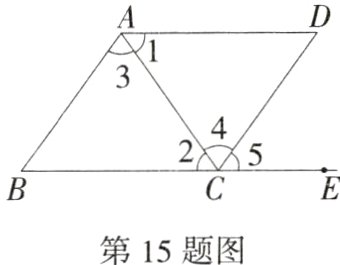
15.(2024湖南邵阳大祥期末)如图,B,C,E三点在同一直线上,要使AB//CD,需要添加的条件是________.(填写1个条件即可)(M7204005)

答案： 答案　∠3=∠4(答案不唯一)
解析　当∠3=∠4时,根据内错角相等，两直线平行可以判定AB//CD.答案不唯一.

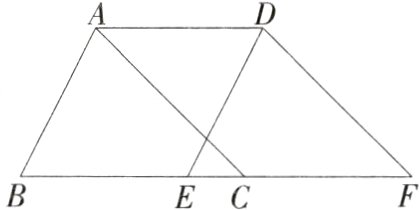
16.如图,将周长为12的三角形ABC沿着射线BC方向平移4个单位后得到三角形DEF,则四边形ABFD的周长等于________.(M7204003)

答案： 答案　20
解析　根据题意，将周长为12的三角形ABC沿边BC向右平移4个单位后得到三角形DEF，
∴AD=4,
BF=BC+CF=BC+4,DF=AC,又
∵AB+BC+AC=12,
∴四边形ABFD的周长=AD+AB+BF+DF=4+AB+BC+4+AC=20.故答案为20.

17.(平行线拐点模型)已知直线a//b,一块含30°角的直角三角尺(∠BCD = 90°,∠B = 30°)按如图所示的方式放置,若∠1 = 34°,则∠2的度数为________.
　

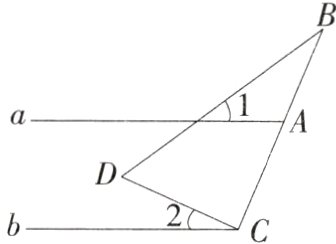
答案：
答案　26°
解析　如图,过D作DM//a,
∵a//b,
∴DM//a//b,
∴∠BDM=∠1=34°,∠2=∠CDM,
∴∠CDM=60°−34°=26°,
∴∠2=26°.
故答案为26°.

18.(新独家原创)(新考向·规律探究试题)在同一平面内有足够多条直线,记作a1,a2,a3,……,an,如果a1⊥a2,a2//a3,a3⊥a4,a4//a5,……,那么a1与a2024的位置关系是________.

答案： 答案　a₁//a₂₀₂₄
解析　由题意知a₁⊥a₂，a₁⊥a₃，a₁//a₄，a₁//a₅，……，易知位置关系以4次为一循环.规律：对于直线aₙ，下标n除以4，当余数为2或3时，直线aₙ与a₁的位置关系为垂直，当余数为1或整除时，直线aₙ与a₁的位置关系为平行，2 024÷4 = 506，所以a₁//a₂₀₂₄.

19.(8分)如图,直线AB,CD相交于点O,OC平分∠AOM,且∠AOM = 88°,射线ON在∠BOM 的内部.
(1)求∠AOD的度数.
(2)若∠BOC = 4∠NOB,求∠MON的度数.

答案： 解析　
(1)
∵OC平分∠AOM,且∠AOM=88°,
∴∠AOC=∠COM= $\frac{1}{2}$∠AOM = 44°，
∴∠AOD=180°−44°=136°.
(2)
∵∠AOD=136°,
∴∠BOC=136°,
∵∠BOC=4∠NOB,
∴∠NOB=34°,
∵∠COM=44°,
∴∠MON=∠BOC−∠NOB−∠COM=136°−34°−44°=58°.