第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
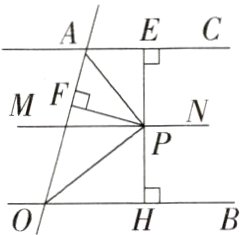
9.如图,直线AC//MN//OB.直线MN上一点P到直线AC、AO、OB的距离相等,即PE = PF = PH.直线AC与MN的距离和直线OB与MN的距离相等吗? 请说明理由.(M7204007)

答案:
解析 相等.理由:
∵PE和PH的长分别是直线AC与MN的距离和直线OB与MN的距离,且PE = PH,
∴直线AC与MN的距离和直线OB与MN的距离相等.
∵PE和PH的长分别是直线AC与MN的距离和直线OB与MN的距离,且PE = PH,
∴直线AC与MN的距离和直线OB与MN的距离相等.
10.(2024湖南娄底涟源期末,6,)在同一平面内,a,b,c是三条互相平行的直线,已知a与b之间的距离为4,b与c之间的距离为1,则a与c之间的距离是(M7204007) ( )
A.3
B.5
C.3或5
D.无法确定
A.3
B.5
C.3或5
D.无法确定
答案:
C ①当直线c在直线a、b的同一侧时,如图1,
∵a与b之间的距离为4,b与c之间的距离为1,
∴a与c之间的距离为4 + 1 = 5;
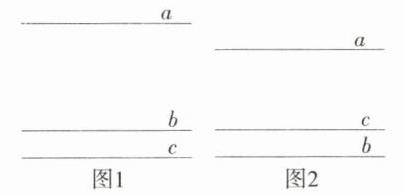
②当直线c在直线a、b之间时,如图2,
∵a与b之间的距离为4,b与c之间的距离为1,
∴a与c之间的距离为4 - 1 = 3.
综上,a与c之间的距离为3或5,故选C.
C ①当直线c在直线a、b的同一侧时,如图1,
∵a与b之间的距离为4,b与c之间的距离为1,
∴a与c之间的距离为4 + 1 = 5;

②当直线c在直线a、b之间时,如图2,
∵a与b之间的距离为4,b与c之间的距离为1,
∴a与c之间的距离为4 - 1 = 3.
综上,a与c之间的距离为3或5,故选C.
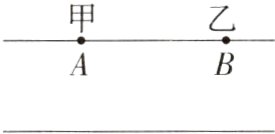
11.(2023湖南常德桃源期末,15,)如图,甲、乙两只蚂蚁分别在两条平行马路同一侧的A,B两点处,比赛看谁先横过马路.如果它们同时出发,速度一样,都走最近的道路,结果是__________,依据是____________________.(M7204007)

答案:
答案 同时到达;平行线间的距离处处相等
解析
∵垂线段最短,
∴两只蚂蚁走的都是垂线段,
∵平行线间的距离处处相等,它们同时出发,速度一样,
∴它们同时到达.
解析
∵垂线段最短,
∴两只蚂蚁走的都是垂线段,
∵平行线间的距离处处相等,它们同时出发,速度一样,
∴它们同时到达.
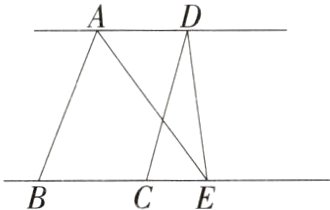
12.(2024河北沧州青县期末,14,)如图,AD//BC,CE = 3,BE = 8,三角形DCE的面积为6,则三角形ABE的面积为________.(M7204007)

答案:
答案 16
解析 如图,作DG⊥BE于G,AH⊥BC于H,
∵AD//BC,
∴AH = DG,
∵三角形DCE的面积为6,CE = 3,
∴DG = AH = 4,
∴三角形ABE的面积=$\frac{1}{2}BE\cdot AH = 16$.

答案 16
解析 如图,作DG⊥BE于G,AH⊥BC于H,
∵AD//BC,
∴AH = DG,
∵三角形DCE的面积为6,CE = 3,
∴DG = AH = 4,
∴三角形ABE的面积=$\frac{1}{2}BE\cdot AH = 16$.

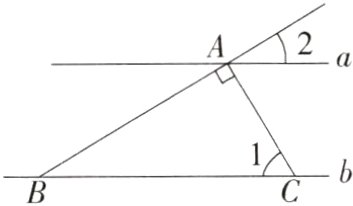
13.(2023湖南张家界永定期末,21,)如图,直线a//b,AB与a,b分别相交于点A,B,且AC⊥AB交直线b于点C.(M7204007)
(1)若∠1 = 60°,求∠2的度数.
(2)若AC = 5,AB = 12,BC = 13,求直线a与b之间的距离.
(1)若∠1 = 60°,求∠2的度数.
(2)若AC = 5,AB = 12,BC = 13,求直线a与b之间的距离.

答案:
解析
(1)如图,
∵直线a//b,
∴∠3 = ∠1 = 60°,又
∵AC⊥AB,
∴∠2 = 90° - ∠3 = 30°.

(2)如图,过A作AD⊥BC于D,则AD的长为直线a与b之间的距离.
∵$S_{\triangle ABC}=\frac{1}{2}AB\cdot AC=\frac{1}{2}BC\cdot AD$,
∴$AD=\frac{AB\cdot AC}{BC}=\frac{12\times5}{13}=\frac{60}{13}$,
∴直线a与b之间的距离为$\frac{60}{13}$.
解析
(1)如图,
∵直线a//b,
∴∠3 = ∠1 = 60°,又
∵AC⊥AB,
∴∠2 = 90° - ∠3 = 30°.

(2)如图,过A作AD⊥BC于D,则AD的长为直线a与b之间的距离.
∵$S_{\triangle ABC}=\frac{1}{2}AB\cdot AC=\frac{1}{2}BC\cdot AD$,
∴$AD=\frac{AB\cdot AC}{BC}=\frac{12\times5}{13}=\frac{60}{13}$,
∴直线a与b之间的距离为$\frac{60}{13}$.
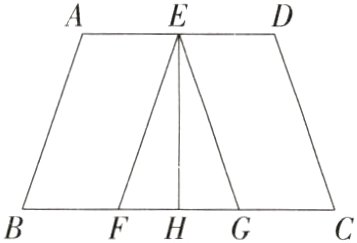
14.推理能力 如图,已知AD//BC,AB//EF,CD//EG,∠A = ∠D,点E在直线AD上,点F,H,G在直线BC上,EH平分∠FEG,线段EH的长是不是两条平行线AD,BC之间的距离? 为什么? (M7204007)

答案:
解析 线段EH的长是两条平行线AD,BC之间的距离.理由:
∵AB//EF,CD//EG,
∴∠AEF + ∠A = 180°,∠DEG + ∠D = 180°,
∵∠A = ∠D,
∴∠AEF = ∠DEG,
∵EH平分∠FEG,
∴∠FEH = ∠GEH,
∴∠AEF + ∠FEH=$\frac{1}{2}\times180^{\circ}=90^{\circ}$,即∠AEH = 90°,
∴EH⊥AD,
∴线段EH的长是两条平行线AD,BC之间的距离.
∵AB//EF,CD//EG,
∴∠AEF + ∠A = 180°,∠DEG + ∠D = 180°,
∵∠A = ∠D,
∴∠AEF = ∠DEG,
∵EH平分∠FEG,
∴∠FEH = ∠GEH,
∴∠AEF + ∠FEH=$\frac{1}{2}\times180^{\circ}=90^{\circ}$,即∠AEH = 90°,
∴EH⊥AD,
∴线段EH的长是两条平行线AD,BC之间的距离.
查看更多完整答案,请扫码查看


