第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
7. 情境题·现实生活 为了方便市民绿色出行和锻炼身体,政府倡导大家使用共享单车.图 1 是一辆共享单车的实物图,图 2 是其示意图,其中 AB,CD 都与地面 l 平行,∠BCD = 55°,∠BAC = 52°.当∠MAC 等于多少度时,AM 与 BC 平行?




答案:
解析 由题意知AB//CD,
∴∠BAC + ∠ACD = 180°,即∠BAC + ∠ACB + ∠BCD = 180°,
∵∠BCD = 55°,∠BAC = 52°,
∴∠ACB = 73°,
∴当∠MAC = ∠ACB = 73°时,AM//BC.
∴∠BAC + ∠ACD = 180°,即∠BAC + ∠ACB + ∠BCD = 180°,
∵∠BCD = 55°,∠BAC = 52°,
∴∠ACB = 73°,
∴当∠MAC = ∠ACB = 73°时,AM//BC.
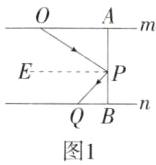
8.(2024 广东茂名高州期末)【阅读探究】如图 1,已知 AB//CD,E、F 分别是 AB、CD 上的点,点 M 在 AB、CD 两平行线之间,∠AEM = 45°,∠CFM = 25°,求∠EMF 的度数.

解:如图 1,过点 M 作 MN//AB,
∵ AB//CD,∴ MN//AB//CD,
∴ ∠EMN = ∠AEM = 45°,∠FMN = ∠CFM = 25°,
∴ ∠EMF = ∠EMN + ∠FMN = 45°+25° = 70°.
从上面的推理过程,我们发现平行线具有“等角转化”的功能,将∠AEM 和∠CFM“凑”在一起,得出∠EMF 的度数,使问题得以解决.
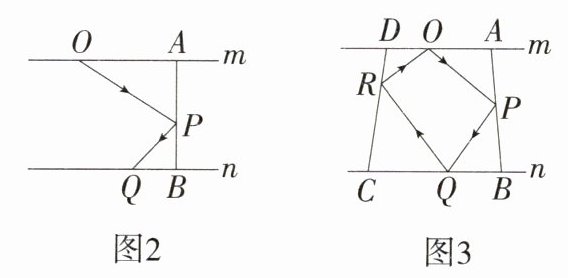
【方法运用】如图 2,已知直线 m//n,AB 是一个平面镜,光线从直线 m 上的点 O 射出,在平面镜 AB 上的点 P 处反射后,经过直线 n 上的点 Q,我们称 OP 为入射光线,PQ 为反射光线,镜面反射有如下性质:入射光线与平面镜的夹角等于反射光线与平面镜的夹角,即∠OPA = ∠QPB.
(1)由图 2 写出∠AOP、∠BQP、∠OPQ 之间的数量关系,并说明理由.
(2)如图 3,再放置 3 块平面镜,其中两块平面镜在直线 m 和 n 上,另一块在两直线之间,四块平面镜构成四边形 ABCD,光线从点 O 以适当的角度射出后,其传播路径为 O→P→Q→R→O→P→…,直接写出∠OPQ 和∠ORQ 的数量关系.
【应用拓展】
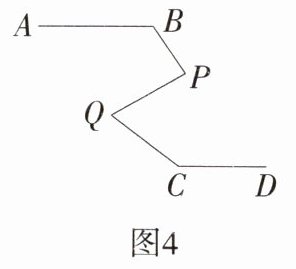
问题情境:“公路村村通”的政策让公路修到了山里,蜿蜒的盘山公路连接了山里与山外的世界.数学活动课上,老师把山路抽象成如图 4 所示的几何图形,并提出了一个问题:在图 4 中,AB//CD,∠B = 125°,∠PQC = 65°,∠C = 145°,求∠BPQ 的度数.请你帮忙解答一下吧.

解:如图 1,过点 M 作 MN//AB,
∵ AB//CD,∴ MN//AB//CD,
∴ ∠EMN = ∠AEM = 45°,∠FMN = ∠CFM = 25°,
∴ ∠EMF = ∠EMN + ∠FMN = 45°+25° = 70°.
从上面的推理过程,我们发现平行线具有“等角转化”的功能,将∠AEM 和∠CFM“凑”在一起,得出∠EMF 的度数,使问题得以解决.
【方法运用】如图 2,已知直线 m//n,AB 是一个平面镜,光线从直线 m 上的点 O 射出,在平面镜 AB 上的点 P 处反射后,经过直线 n 上的点 Q,我们称 OP 为入射光线,PQ 为反射光线,镜面反射有如下性质:入射光线与平面镜的夹角等于反射光线与平面镜的夹角,即∠OPA = ∠QPB.
(1)由图 2 写出∠AOP、∠BQP、∠OPQ 之间的数量关系,并说明理由.
(2)如图 3,再放置 3 块平面镜,其中两块平面镜在直线 m 和 n 上,另一块在两直线之间,四块平面镜构成四边形 ABCD,光线从点 O 以适当的角度射出后,其传播路径为 O→P→Q→R→O→P→…,直接写出∠OPQ 和∠ORQ 的数量关系.
【应用拓展】
问题情境:“公路村村通”的政策让公路修到了山里,蜿蜒的盘山公路连接了山里与山外的世界.数学活动课上,老师把山路抽象成如图 4 所示的几何图形,并提出了一个问题:在图 4 中,AB//CD,∠B = 125°,∠PQC = 65°,∠C = 145°,求∠BPQ 的度数.请你帮忙解答一下吧.


答案:
解析 【方法运用】
(1)∠OPQ = ∠AOP + ∠BQP,理由如下:
如图1,过点P作PE//OA,则PE//BQ,∠AOP = ∠OPE,
∴∠BQP = ∠QPE,
∵∠OPQ = ∠OPE + ∠QPE,
∴∠OPQ = ∠AOP + ∠BQP.
(2)∠OPQ = ∠ORQ.
详解:由
(1)得,∠AOP + ∠BQP = ∠OPQ,同理可得,∠DOR + ∠CQR = ∠ORQ,由镜面反射的性质可得∠AOP = ∠DOR,∠BQP = ∠CQR,
∴∠OPQ = ∠ORQ.
【应用拓展】
如图2,过点P作PM//AB,过点Q作QN//AB,则AB//PM//QN//CD,
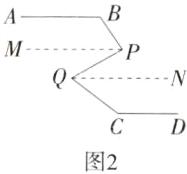
∴∠ABP + ∠BPM = 180°,∠MPQ = ∠PQN,∠DCQ + ∠CQN = 180°,
∵∠B = 125°,∠C = 145°,
∴∠BPM = 180° - 125° = 55°,∠CQN = 180° - 145° = 35°,
∵∠PQC = 65°,
∴∠PQN = ∠PQC - ∠CQN = 65° - 35° = 30°,
∴∠QPM = ∠PQN = 30°,
∴∠BPQ = ∠BPM + ∠QPM = 55° + 30° = 85°.
解析 【方法运用】
(1)∠OPQ = ∠AOP + ∠BQP,理由如下:
如图1,过点P作PE//OA,则PE//BQ,∠AOP = ∠OPE,
∴∠BQP = ∠QPE,
∵∠OPQ = ∠OPE + ∠QPE,
∴∠OPQ = ∠AOP + ∠BQP.

(2)∠OPQ = ∠ORQ.
详解:由
(1)得,∠AOP + ∠BQP = ∠OPQ,同理可得,∠DOR + ∠CQR = ∠ORQ,由镜面反射的性质可得∠AOP = ∠DOR,∠BQP = ∠CQR,
∴∠OPQ = ∠ORQ.
【应用拓展】
如图2,过点P作PM//AB,过点Q作QN//AB,则AB//PM//QN//CD,

∴∠ABP + ∠BPM = 180°,∠MPQ = ∠PQN,∠DCQ + ∠CQN = 180°,
∵∠B = 125°,∠C = 145°,
∴∠BPM = 180° - 125° = 55°,∠CQN = 180° - 145° = 35°,
∵∠PQC = 65°,
∴∠PQN = ∠PQC - ∠CQN = 65° - 35° = 30°,
∴∠QPM = ∠PQN = 30°,
∴∠BPQ = ∠BPM + ∠QPM = 55° + 30° = 85°.
查看更多完整答案,请扫码查看


