《2025年5年中考3年模拟七年级数学下册湘教版》

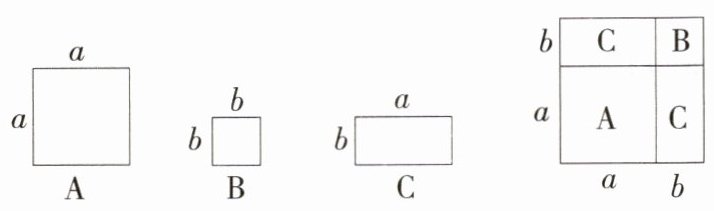
9.(2023湖北随州中考,9,)如图,有足够多的边长分别为$a$和$b(a＞b)$的A类和B类正方形纸片,以及长为$a$、宽为$b$的C类长方形纸片.要拼一个边长为$a + b$的正方形,需要1张A类纸片、1张B类纸片和2张C类纸片.若要拼一个长为$3a + b$、宽为$2a + 2b$的长方形,则需要C类纸片的张数为(M7201002) ( )


A.6
B.7
C.8
D.9

答案： C $\because(3a + b)(2a + 2b)=6a^{2}+6ab + 2ab + 2b^{2}=6a^{2}+8ab+2b^{2}$,$\therefore$若要拼一个长为$3a + b$、宽为$2a + 2b$的长方形, 则需要C类纸片的张数为8. 故选C.

10.[新考法] (2024重庆二模,10,)对于多项式:$x + 1,x + 3,2x + 2,2x + 6$,用任意两个多项式的积,再与剩余的两个多项式的积作差,并算出结果,称之为“积差操作”.例如:$(x + 1)(x + 3)-(2x + 2)(2x + 6)=-3x^{2}-12x - 9$,下列说法:
①一定存在一种“积差操作”使得操作后的结果,无论$x$取何值,都为3的倍数;
②不存在任何“积差操作”,使其结果为0;
③所有的“积差操作”共有5种不同的结果.
其中正确说法的个数是(M7201002) ( )
A.0
B.1
C.2
D.3

答案： C 本题以新概念的形式考查多项式的乘法运算.
$(x + 1)(x + 3)-(2x + 2)(2x + 6)=-3x^{2}-12x - 9=3(-x^{2}-4x - 3)$, 故①正确;$(x + 1)(2x + 6)-(x + 3)(2x + 2)=0$, 故②错误;
$(x + 1)(x + 3)-(2x + 2)(2x + 6)=-3x^{2}-12x - 9$,
$(x + 1)(2x + 2)-(x + 3)(2x + 6)=-8x - 16$,
$(x + 1)(2x + 6)-(x + 3)(2x + 2)=0$,
$(x + 3)(2x + 2)-(x + 1)(2x + 6)=0$,
$(x + 3)(2x + 6)-(x + 1)(2x + 2)=8x + 16$,
$(2x + 2)(2x + 6)-(x + 1)(x + 3)=3x^{2}+12x + 9$,
共5种不同结果, 故③正确. 故选C.

11.(2024安徽淮北五校联考期末,18,★)如果关于$x$的多项式$x - 2$与$x^{2}+mx + 1$的乘积中不含$x$的一次项,求$m$的值.(M7201002)

答案： 解析 $(x - 2)(x^{2}+mx + 1)=x^{3}+mx^{2}+x - 2x^{2}-2mx - 2=x^{3}+(m - 2)x^{2}+(1 - 2m)x - 2$,$\because$关于$x$的多项式$x - 2$与$x^{2}+mx + 1$的乘积中不含$x$的一次项,$\therefore 1 - 2m = 0$,解得$m=\frac{1}{2}$,$\therefore m$的值为$\frac{1}{2}$.

12.运算能力 观察以下等式:
$(x + 1)(x^{2}-x + 1)=x^{3}+1$;
$(x + 3)(x^{2}-3x + 9)=x^{3}+27$;
$(x + 6)(x^{2}-6x + 36)=x^{3}+216$;
……
(1)按以上等式的规律填空:
$(a + b)$(________)$=a^{3}+$________.
(2)利用多项式的乘法法则,说明(1)中的等式成立.
(3)利用(1)中的规律化简:$(x + y)(x^{2}-xy + y^{2})-(x + 2y)(x^{2}-2xy + 4y^{2})$.

答案： 解析
(1)$a^{2}-ab + b^{2}$;$b^{3}$.
(2)$(a + b)(a^{2}-ab + b^{2})=a^{3}-a^{2}b + ab^{2}+a^{2}b - ab^{2}+b^{3}=a^{3}+b^{3}$.
(3)原式$=(x^{3}+y^{3})-(x^{3}+8y^{3})=-7y^{3}$.

1.要使$-x^{3}(x^{2}+ax + 1)+2x^{4}$中不含$x$的四次项,则$a =$ ( )
A.1
B.2
C.3
D.4

答案： B 原式$=-x^{5}-ax^{4}-x^{3}+2x^{4}=-x^{5}+(2 - a)x^{4}-x^{3}$,$\because -x^{3}(x^{2}+ax + 1)+2x^{4}$中不含$x$的四次项,$\therefore 2 - a = 0$, 解得$a = 2$. 故选B.

2.若$x + m$与$x + 2$的乘积中不含$x$的一次项,则$m$的值为 ( )
A.2
B.1
C.0
D.-2

答案： D $(x + m)(x + 2)=x^{2}+(2 + m)x + 2m$,$\because x + m$与$x + 2$的乘积中不含$x$的一次项,$\therefore 2 + m = 0$, 解得$m=-2$. 故选D.

3.若$(x^{2}+mx + 8)(x^{2}-3x + n)$的展开式中不含$x^{3}$项和$x^{2}$项,则$m^{n}=$ ( )
A.-4
B.3
C.4
D.6

答案： B $(x^{2}+mx + 8)(x^{2}-3x + n)=x^{4}-3x^{3}+nx^{2}+mx^{3}-3mx^{2}+mnx + 8x^{2}-24x + 8n=x^{4}+(m - 3)x^{3}+(n - 3m + 8)x^{2}+(mn - 24)x + 8n$,$\because(x^{2}+mx + 8)(x^{2}-3x + n)$的展开式中不含$x^{3}$项和$x^{2}$项,$\therefore\begin{cases}m - 3 = 0,\\n - 3m + 8 = 0,\end{cases}$解得$\begin{cases}m = 3,\\n = 1,\end{cases}$$\therefore m^{n}=3^{1}=3$. 故选B.