《2025年5年中考3年模拟七年级数学下册湘教版》

1.(2023湖南衡阳中考)计算$(\frac{1}{2}x^{3})^{2}$的结果正确的是(M7201001) (　　)
A.$x^{6}$
B.$\frac{1}{4}x^{6}$
C.$\frac{1}{4}x^{5}$
D.$x^{9}$

答案： B 原式=($\frac{1}{2}$)²(x³)²=$\frac{1}{4}$x⁶.

2.计算$2a(a - 1) - a(2a + 3)$的结果为 (　　)
A.$a$
B.$5a$
C.$-5a$
D.$3a$

答案： C 原式=2a² - 2a - 2a² - 3a = -5a.

3.[新独家原创]若$(x - 2025)(x + 2024)=x^{2}+mx - 2025×2024$,则$m$的值为 (　　)
A.1
B.-1
C.2025
D.-2025

答案： B (x - 2025)(x + 2024)=x² + 2024x - 2025x - 2025×2024=x² - x - 2025×2024,所以m = -1.

4.若$(x - 3)^{2}=x^{2}+ax + 9$,则$a$的值为 (　　)
A.-6
B.-3
C.3
D.6

答案： A
∵(x - 3)²=x² - 6x + 9=x² + ax + 9,
∴a = -6,故选A.

5.(2024湖南永州江永期中)下列选项中,不能运用平方差公式进行运算的是(M7201003) (　　)
A.$(x + a)(x - a)$
B.$(a + b)(-a - b)$
C.$(-x - b)(x - b)$
D.$(b + m)(m - b)$

答案： B 根据平方差公式的特点解题.

6.某青少年活动中心的场地为长方形,原来的长为$a$,宽为$b$.现在要把四周都向外扩建,长增加3,宽增加2,那么这个场地的面积增加 (　　)
A.6
B.3a - 2b
C.2a + 3b + 6
D.3a + 2b + 6

答案： C 由题意,得(a + 3)(b + 2) - ab=ab + 3b + 2a + 6 - ab=2a + 3b + 6.故选C.

7.(2024湖南长沙望城期中)若$a = 81^{31},b = 27^{41},c = 9^{61}$,则$a,b,c$的大小关系是(M7201001) (　　)
A.$c\lt b\lt a$
B.$b\lt c\lt a$
C.$c\lt a\lt b$
D.$a\lt c\lt b$

答案： A
∵a = 81³¹=(3⁴)³¹=3¹²⁴,b = 27⁴¹=(3³)⁴¹=3¹²³,c = 9⁶¹=(3²)⁶¹=3¹²²,122＜123＜124,
∴c＜b＜a.故选A.

8.下列运算:①$(-x^{2})^{3}=x^{5}$;②$(-2a^{3}b^{4})^{3}=-8a^{9}b^{12}$;③$3^{100}×(-3)^{100}=0$;④$m\cdot m^{5}\cdot m^{7}=m^{12}$;⑤$3a^{4}+a^{4}=3a^{8}$;⑥$(x^{2})^{4}=x^{16}$. 其中正确的个数是(M7201001) (　　)
A.1
B.2
C.3
D.4

答案： A ①(-x²)³=-x⁶,故①错误;②(-2a³b⁴)³=-8a⁹b¹²,故②正确;③3¹⁰⁰×(-3)¹⁰⁰=9¹⁰⁰,故③错误;④m·m⁵·m⁷=m¹³,故④错误;⑤3a⁴ + a⁴=4a⁴,故⑤错误;⑥(x²)⁴=x⁸,故⑥错误.综上,正确的个数是1.故选A.

9.[数形结合思想]4张长为$a$、宽为$b(a＞b)$的长方形纸片,按如图所示的方式拼成一个边长为$a + b$的正方形,图中空白部分的面积为$S_{1}$,阴影部分的面积为$S_{2}$.若$S_{1}=2S_{2}$,则$a、b$满足的关系式为 (　　)

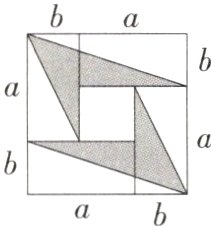
A.2a = 5b
B.2a = 3b
C.a = 3b
D.a = 2b

答案： D S₁=$\frac{1}{2}$b(a + b)×2 + $\frac{1}{2}$ab×2 + (a - b)²=a² + 2b²,S₂=(a + b)² - S₁=(a + b)² - (a² + 2b²)=2ab - b²,
∵S₁ = 2S₂,
∴a² + 2b²=2(2ab - b²),整理得(a - 2b)²=0,
∴a - 2b = 0,
∴a = 2b.故选D.

10.[新考向·规律探究试题]$(x - 1)(x + 1)=x^{2}-1$,$(x - 1)(x^{2}+x + 1)=x^{3}-1$,$(x - 1)(x^{3}+x^{2}+x + 1)=x^{4}-1$,$(x - 1)(x^{4}+x^{3}+x^{2}+x + 1)=x^{5}-1$,$\cdots\cdots$,依此规律,可以得出$2^{2022}+2^{2021}+2^{2020}+\cdots+2^{3}+2^{2}+2 + 1$的末位数字是 (　　)
A.7
B.5
C.3
D.1

答案： A 由题中的规律可知(x - 1)(x²⁰²² + x²⁰²¹ +... + x² + x + 1)=x²⁰²³ - 1,
将x = 2代入得(2 - 1)×(2²⁰²² + 2²⁰²¹ +... + 2² + 2 + 1)=2²⁰²³ - 1,则2²⁰²² + 2²⁰²¹ +... + 2² + 2 + 1=2²⁰²³ - 1,因为2¹ - 1 = 1,2² - 1 = 3,2³ - 1 = 7,2⁴ - 1 = 15,2⁵ - 1 = 31,……,所以2ⁿ - 1的末位数字以1,3,7,5为一组循环,因为2023÷4 = 505……3,所以2²⁰²³ - 1的末位数字与2³ - 1的末位数字相同,为7.故选A.

11.(2023天津中考)计算$(xy^{2})^{2}$的结果为______.

答案： 答案 x²y⁴
解析 (xy²)²=x²·(y²)²=x²y⁴.

12.(2024湖南郴州桂阳期中)计算:$2m^{2}\cdot3m^{3}=$________.(M7201002)

答案： 答案 6m⁵
解析 原式=(2×3)(m²·m³)=6m⁵,故答案为6m⁵.

13.[新独家原创]计算:$(-8)^{2025}×(-0.125)^{2024}=$________.(M7201001)

答案： 答案 -8
解析 (-8)²⁰²⁵×(-0.125)²⁰²⁴=(-8)²⁰²⁴×0.125²⁰²⁴×(-8)=8²⁰²⁴×0.125²⁰²⁴×(-8)=(8×0.125)²⁰²⁴×(-8)=1²⁰²⁴×(-8)=1×(-8)= -8.故答案为-8.

14.(2023四川凉山州中考)已知$y^{2}-my + 1$是完全平方式,则$m$的值是________.(M7201003)

答案： 答案 ±2
解析
∵y² - my + 1是完全平方式,y² - 2y + 1=(y - 1)²,y² + 2y + 1=(y + 1)²,
∴ -m = -2或 -m = 2,
∴m = 2或m = -2,故答案为±2.

15.计算:$x^{2}\cdot x^{4}+(-3x^{3})^{2}+(-2x^{2})^{3}=$________.

答案： 答案 2x⁶
解析 x²·x⁴ + (-3x³)² + (-2x²)³=x⁶ + 9x⁶ - 8x⁶=2x⁶.

16.(2024广西柳州期中)某同学在计算一个多项式$A$乘$(1 - 3x^{2})$时,因抄错运算符号,算成了加上$(1 - 3x^{2})$,得到的结果是$x^{2}-3x + 1$,正确的计算结果是______________.(M7201002)

答案： 答案 4x² - 12x⁴ - 3x + 9x³
解析 根据题意可知A + (1 - 3x²)=x² - 3x + 1,
∴A=x² - 3x + 1 - (1 - 3x²)=x² - 3x + 1 - 1 + 3x²=4x² - 3x,
∴(4x² - 3x)(1 - 3x²)=4x² - 12x⁴ - 3x + 9x³.故答案为4x² - 12x⁴ - 3x + 9x³.

17.把20 cm长的一根铁丝分成两段,将每段都围成一个正方形,若这两个正方形的面积之差是5 cm²,则这两段铁丝的长分别为________.

答案： 答案 12 cm,8 cm(不分前后顺序)
解析 设其中较长的一段铁丝的长为x cm,则另一段铁丝的长为(20 - x)cm,根据题意得($\frac{x}{4}$)² - ($\frac{20 - x}{4}$)²=5,解得x = 12,则20 - x = 20 - 12 = 8,所以这两段铁丝的长分别为12 cm,8 cm.