第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
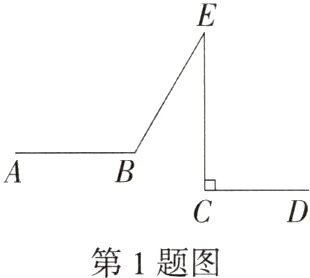
1.(2022安徽黄山期末)如图所示,AB//CD,EC⊥CD.若∠BEC = 30°,则∠ABE的度数为 ( )
A.100°
B.110°
C.120°
D.130°

A.100°
B.110°
C.120°
D.130°
答案:
A 如图,过点E作EG//AB,
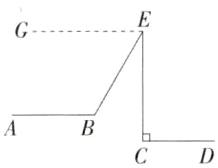
因为AB//CD,所以EG//CD,所以∠GEC = ∠DCE.
因为EC⊥CD,所以∠GEC = ∠DCE = 90°,
因为∠BEC = 30°,所以∠GEB = 90° - 30° = 60°,
因为EG//AB,所以∠ABE + ∠GEB = 180°,
所以∠ABE = 180° - 60° = 120°.
A 如图,过点E作EG//AB,

因为AB//CD,所以EG//CD,所以∠GEC = ∠DCE.
因为EC⊥CD,所以∠GEC = ∠DCE = 90°,
因为∠BEC = 30°,所以∠GEB = 90° - 30° = 60°,
因为EG//AB,所以∠ABE + ∠GEB = 180°,
所以∠ABE = 180° - 60° = 120°.
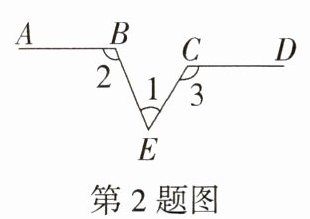
2.如图,已知AB//CD,若∠1 = 50°,∠2 = 110°,则∠3 = ______°.

答案:
答案 120
解析 如图,过E作EF//CD.
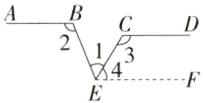
∵AB//CD,EF//CD,
∴AB//EF,
∴∠2 = ∠1 + ∠4 = 110°,
∵∠1 = 50°,
∴∠4 = 60°,
∵EF//CD,
∴∠3 + ∠4 = 180°,
∴∠3 = 120°.故答案为120.
答案 120
解析 如图,过E作EF//CD.

∵AB//CD,EF//CD,
∴AB//EF,
∴∠2 = ∠1 + ∠4 = 110°,
∵∠1 = 50°,
∴∠4 = 60°,
∵EF//CD,
∴∠3 + ∠4 = 180°,
∴∠3 = 120°.故答案为120.
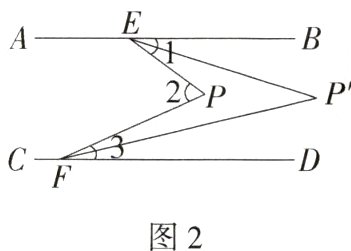
3.直线AB//CD,点P在两平行线之间,点E、F分别在AB、CD上,连接PE、PF.
(1)若图1中∠1 = 36°,∠2 = 60°,则∠3 = ______.
(2)探究图1中∠1,∠2与∠3之间的数量关系,并说明理由.
(3)如图2所示,∠1与∠3的平分线交于点P',若∠2 = α,试求∠EP'F的度数(用含α的代数式表示).

(1)若图1中∠1 = 36°,∠2 = 60°,则∠3 = ______.
(2)探究图1中∠1,∠2与∠3之间的数量关系,并说明理由.
(3)如图2所示,∠1与∠3的平分线交于点P',若∠2 = α,试求∠EP'F的度数(用含α的代数式表示).


答案:
解析
(1)24°.
(2)∠2 = ∠1 + ∠3.理由:如图,过P作PM//AB.

因为AB//CD,AB//PM,所以PM//CD//AB,
所以∠1 = ∠MPE,∠3 = ∠MPF,
所以∠EPF = ∠MPE + ∠MPF = ∠1 + ∠3,
即∠2 = ∠1 + ∠3.
(3)因为EP'平分∠BEP,FP'平分∠DFP,
所以∠BEP' = $\frac{1}{2}$∠BEP,∠DFP' = $\frac{1}{2}$∠DFP,
因为∠BEP + ∠DFP = ∠2 = α,所以∠EP'F = ∠BEP' + ∠DFP' = $\frac{1}{2}$(∠BEP + ∠DFP) = $\frac{1}{2}$α.
解析
(1)24°.
(2)∠2 = ∠1 + ∠3.理由:如图,过P作PM//AB.

因为AB//CD,AB//PM,所以PM//CD//AB,
所以∠1 = ∠MPE,∠3 = ∠MPF,
所以∠EPF = ∠MPE + ∠MPF = ∠1 + ∠3,
即∠2 = ∠1 + ∠3.
(3)因为EP'平分∠BEP,FP'平分∠DFP,
所以∠BEP' = $\frac{1}{2}$∠BEP,∠DFP' = $\frac{1}{2}$∠DFP,
因为∠BEP + ∠DFP = ∠2 = α,所以∠EP'F = ∠BEP' + ∠DFP' = $\frac{1}{2}$(∠BEP + ∠DFP) = $\frac{1}{2}$α.
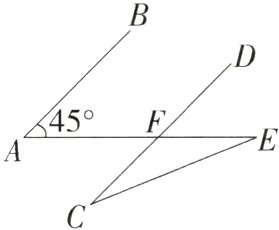
4.(2022福建厦门一中期中)如图,AB//CD,∠A = 45°,∠E = 22°,则∠C的度数为 ( )
A.25°
B.45°
C.23°
D.22°

A.25°
B.45°
C.23°
D.22°
答案:
C 如图,过E作EG//AB,
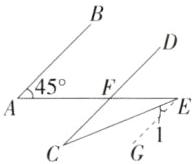
因为AB//CD,所以EG//CD,所以∠1 = ∠C.
因为EG//AB,∠A = 45°,
所以∠AEG = ∠A = 45°,
所以∠1 = ∠AEG - ∠FEC = 45° - 22° = 23°,
所以∠C = 23°.
C 如图,过E作EG//AB,

因为AB//CD,所以EG//CD,所以∠1 = ∠C.
因为EG//AB,∠A = 45°,
所以∠AEG = ∠A = 45°,
所以∠1 = ∠AEG - ∠FEC = 45° - 22° = 23°,
所以∠C = 23°.
5.如图1,已知AB//CD,探究∠BED与∠B+∠D的关系:
过E作EM//AB,∴∠1 = ∠B.
∵EM//AB,AB//CD,∴EM//CD,∴∠2 = ∠D,
∴∠1+∠2 = ∠B+∠D.
又∵∠BED = ∠1+∠2,∴∠BED = ∠B+∠D.
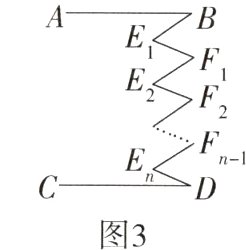
(1)如图2,已知AB//CD,试探究∠E+∠G与∠B+∠F+∠D的关系,并写出推理过程.
(2)如图3,已知AB//CD,请直接写出你能得到的结论.


过E作EM//AB,∴∠1 = ∠B.
∵EM//AB,AB//CD,∴EM//CD,∴∠2 = ∠D,
∴∠1+∠2 = ∠B+∠D.
又∵∠BED = ∠1+∠2,∴∠BED = ∠B+∠D.
(1)如图2,已知AB//CD,试探究∠E+∠G与∠B+∠F+∠D的关系,并写出推理过程.
(2)如图3,已知AB//CD,请直接写出你能得到的结论.



答案:
解析
(1)∠E + ∠G = ∠B + ∠EFG + ∠D.
如图,过F作FN//AB.

由题干中的推理可知
∠E = ∠B + ∠1,∠G = ∠2 + ∠D,
∴∠E + ∠G = ∠B + ∠1 + ∠2 + ∠D,
∴∠E + ∠G = ∠B + ∠EFG + ∠D.
(2)∠E₁ + ∠E₂ + … + ∠Eₙ = ∠B + ∠F₁ + ∠F₂ + … + ∠Fₙ₋₁ + ∠D.
解析
(1)∠E + ∠G = ∠B + ∠EFG + ∠D.
如图,过F作FN//AB.

由题干中的推理可知
∠E = ∠B + ∠1,∠G = ∠2 + ∠D,
∴∠E + ∠G = ∠B + ∠1 + ∠2 + ∠D,
∴∠E + ∠G = ∠B + ∠EFG + ∠D.
(2)∠E₁ + ∠E₂ + … + ∠Eₙ = ∠B + ∠F₁ + ∠F₂ + … + ∠Fₙ₋₁ + ∠D.
查看更多完整答案,请扫码查看


