第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
13.几何直观 已知:直线AB与直线CD交于点O,过点O作OE⊥AB.(M7204006)
(1)如图1,OP为∠AOD内的一条射线,当∠1与∠2满足什么条件时,OP⊥CD?请说明理由.
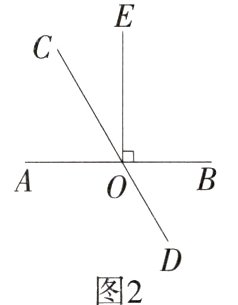
(2)如图2,若∠AOC = $\frac{1}{2}$∠BOC,求∠COE的度数.
(3)如图3,在(2)的条件下,过点O作OF⊥CD,经过点O画直线MN,若射线OM平分∠BOD,请直接写出图中与2∠EOF度数相等的角.


(1)如图1,OP为∠AOD内的一条射线,当∠1与∠2满足什么条件时,OP⊥CD?请说明理由.
(2)如图2,若∠AOC = $\frac{1}{2}$∠BOC,求∠COE的度数.
(3)如图3,在(2)的条件下,过点O作OF⊥CD,经过点O画直线MN,若射线OM平分∠BOD,请直接写出图中与2∠EOF度数相等的角.



答案:
解析
(1)当∠1 = ∠2时,OP⊥CD,理由如下:
∵OE⊥AB,
∴∠AOC + ∠1 = 90°,
∵∠1 = ∠2,
∴∠AOC + ∠2 = ∠COP = 90°,
∴OP⊥CD.
(2)
∵∠AOC + ∠BOC = 180°,且∠AOC = $\frac{1}{2}$∠BOC,
∴∠AOC = 60°,
∵OE⊥AB,
∴∠AOE = 90°,
∴∠COE = 90° - 60° = 30°.
(3)由
(2)知∠AOC = 60°,
∵射线OM平分∠BOD,
∴∠BOM = ∠DOM = ∠AON = ∠CON = 30°,
∵OE⊥AB,OF⊥CD,
∴∠AOE = ∠COF = 90°,
∴∠AOC = ∠EOF = 60°,∠BOF = 180° - 90° - 60° = 30°,
∴∠AOD = ∠BOC = ∠FON = ∠EOM = 180° - 60° = 120° = 2∠EOF,
∴与2∠EOF度数相等的角是∠AOD、∠BOC、∠FON、∠EOM.
(1)当∠1 = ∠2时,OP⊥CD,理由如下:
∵OE⊥AB,
∴∠AOC + ∠1 = 90°,
∵∠1 = ∠2,
∴∠AOC + ∠2 = ∠COP = 90°,
∴OP⊥CD.
(2)
∵∠AOC + ∠BOC = 180°,且∠AOC = $\frac{1}{2}$∠BOC,
∴∠AOC = 60°,
∵OE⊥AB,
∴∠AOE = 90°,
∴∠COE = 90° - 60° = 30°.
(3)由
(2)知∠AOC = 60°,
∵射线OM平分∠BOD,
∴∠BOM = ∠DOM = ∠AON = ∠CON = 30°,
∵OE⊥AB,OF⊥CD,
∴∠AOE = ∠COF = 90°,
∴∠AOC = ∠EOF = 60°,∠BOF = 180° - 90° - 60° = 30°,
∴∠AOD = ∠BOC = ∠FON = ∠EOM = 180° - 60° = 120° = 2∠EOF,
∴与2∠EOF度数相等的角是∠AOD、∠BOC、∠FON、∠EOM.
14.几何直观 O为直线DA上一点,OB⊥OF,OE是∠AOB的平分线.(M77204006)
(1)如图1,若∠AOB = 130°,求∠EOF的度数.
(2)如图1,若∠AOB = α,90°<α<180°,求∠EOF的度数(用含α的代数式表示).
(3)若∠AOB = α,0°<α<90°,请在图2中画出射线OF,使得(2)中∠EOF的结果仍然成立.


(1)如图1,若∠AOB = 130°,求∠EOF的度数.
(2)如图1,若∠AOB = α,90°<α<180°,求∠EOF的度数(用含α的代数式表示).
(3)若∠AOB = α,0°<α<90°,请在图2中画出射线OF,使得(2)中∠EOF的结果仍然成立.


答案:
解析
(1)
∵∠AOB = 130°,OE是∠AOB的平分线,
∴∠AOE = $\frac{1}{2}$∠AOB = $\frac{1}{2}$×130° = 65°,
∵OB⊥OF,
∴∠BOF = 90°,
∴∠AOF = ∠AOB - ∠BOF = 130° - 90° = 40°,
∴∠EOF = ∠AOE - ∠AOF = 65° - 40° = 25°.
(2)
∵∠AOB = α,90° < α < 180°,OE是∠AOB的平分线,
∴∠AOE = $\frac{1}{2}$α,
∵∠BOF = 90°,
∴∠AOF = α - 90°,
∴∠EOF = ∠AOE - ∠AOF = $\frac{1}{2}$α - (α - 90°) = 90° - $\frac{1}{2}$α.
(3)如图,
∵∠AOB = α,
∴∠BOE = ∠AOE = $\frac{1}{2}$α,
∵∠BOF = 90°,
∴∠EOF = ∠BOF - ∠BOE = 90° - $\frac{1}{2}$α.

解析
(1)
∵∠AOB = 130°,OE是∠AOB的平分线,
∴∠AOE = $\frac{1}{2}$∠AOB = $\frac{1}{2}$×130° = 65°,
∵OB⊥OF,
∴∠BOF = 90°,
∴∠AOF = ∠AOB - ∠BOF = 130° - 90° = 40°,
∴∠EOF = ∠AOE - ∠AOF = 65° - 40° = 25°.
(2)
∵∠AOB = α,90° < α < 180°,OE是∠AOB的平分线,
∴∠AOE = $\frac{1}{2}$α,
∵∠BOF = 90°,
∴∠AOF = α - 90°,
∴∠EOF = ∠AOE - ∠AOF = $\frac{1}{2}$α - (α - 90°) = 90° - $\frac{1}{2}$α.
(3)如图,
∵∠AOB = α,
∴∠BOE = ∠AOE = $\frac{1}{2}$α,
∵∠BOF = 90°,
∴∠EOF = ∠BOF - ∠BOE = 90° - $\frac{1}{2}$α.

查看更多完整答案,请扫码查看


