2025年赢在假期期末加寒假八年级数学沪科版合肥工业大学出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年赢在假期期末加寒假八年级数学沪科版合肥工业大学出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
知识3 一次函数
6. 一般把形如________(k,b为常数,且$k\neq0$)的函数叫做一次函数.
6. 一般把形如________(k,b为常数,且$k\neq0$)的函数叫做一次函数.
答案:
6.y=kx十b
7. 正比例函数$y = kx$的图象是经过原点$(0,0)$的一条直线.
答案:
7.是经过原点(0,0)和(1,k)两点的直线
8. 一次函数$y = kx + b$的图象是经过点________的直线,点________是直线$y = kx + b$与y轴的交点. 当________时,此交点在y轴的正半轴上;当________时,此交点在y轴的负半轴上;当________时,此交点在原点,此时的一次函数是正比例函数.
答案:
8.(0,b)(0,b)b>0 b<0
b=0 正比例函数
9. 根据几何知识“两点确定一条直线”,所以画一次函数的图象时,只要先描出两点,再过这两点画直线即可. 在画关于实际问题的一次函数的图象时,要先明确自变量的取值范围,再画图象.
10. 当$k>0$时,一次函数$y = kx + b$的图象是从左到右上升的直线,即y随x的增大而增大;
当$k<0$时,一次函数$y = kx + b$的图象是从左到右下降的直线,即y随x的增大而减小.
10. 当$k>0$时,一次函数$y = kx + b$的图象是从左到右上升的直线,即y随x的增大而增大;
当$k<0$时,一次函数$y = kx + b$的图象是从左到右下降的直线,即y随x的增大而减小.
答案:
例题 已知一次函数$y = (6 + 3m)x + (m - 4)$,y随x的增大而增大,函数的图象与y轴的交点在y轴的负半轴上,求m的取值范围.
分析
根据一次函数的性质可知:$6 + 3m>0$,且$m - 4<0$,解不等式即可.
解 根据题意,得$\begin{cases}6 + 3m>0,\\m - 4<0,\end{cases}$解得$- 2<m<4$.
所以m的取值范围是$- 2<m<4$.
分析
根据一次函数的性质可知:$6 + 3m>0$,且$m - 4<0$,解不等式即可.
解 根据题意,得$\begin{cases}6 + 3m>0,\\m - 4<0,\end{cases}$解得$- 2<m<4$.
所以m的取值范围是$- 2<m<4$.
答案:
10.左 右 增大 左 右
减小
跟踪训练 下列图象中,表示直线$y = x - 1$的是 ( )

[答案] D

[答案] D
答案:
例题 函数$y = \frac{3}{2}x + 3$的图象如图所示,根据图象解答下列问题:
(1)x取什么值时,函数值y不小于0?
(2)x取什么值时,函数的图象在x轴下方?
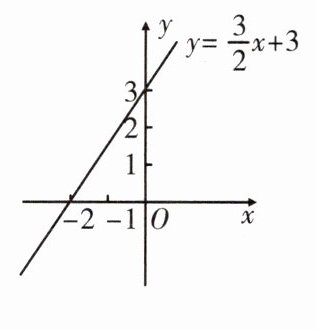
分析
(1)y不小于0的点一定在x轴及其上方,可以把问题转化成解不等式$\frac{3}{2}x + 3\geqslant0$;(2)图象在x轴下方,即函数值$y<0$,可以通过解不等式$\frac{3}{2}x + 3<0$求出.
解 (1)因为$y\geqslant0$,所以$\frac{3}{2}x + 3\geqslant0$. 解得$x\geqslant - 2$. 即当$x\geqslant - 2$时,函数值y不小于0. (2)因为图象在x轴下方,所以$y<0$,即$\frac{3}{2}x + 3<0$. 解得$x< - 2$.
(1)x取什么值时,函数值y不小于0?
(2)x取什么值时,函数的图象在x轴下方?
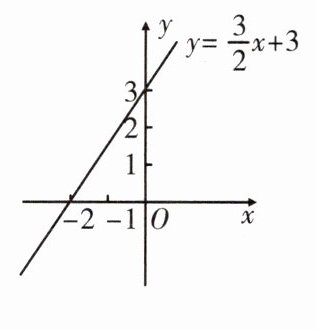
分析
(1)y不小于0的点一定在x轴及其上方,可以把问题转化成解不等式$\frac{3}{2}x + 3\geqslant0$;(2)图象在x轴下方,即函数值$y<0$,可以通过解不等式$\frac{3}{2}x + 3<0$求出.
解 (1)因为$y\geqslant0$,所以$\frac{3}{2}x + 3\geqslant0$. 解得$x\geqslant - 2$. 即当$x\geqslant - 2$时,函数值y不小于0. (2)因为图象在x轴下方,所以$y<0$,即$\frac{3}{2}x + 3<0$. 解得$x< - 2$.
答案:
查看更多完整答案,请扫码查看


