《2025年赢在假期期末加寒假八年级数学沪科版合肥工业大学出版社》

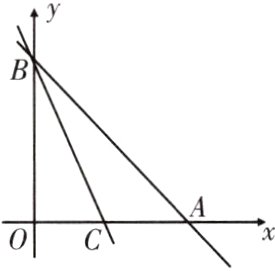
17. 如图，已知直线$y = -x + 2$与$x$轴、$y$轴分别交于点$A$和点$B$，另一直线$y = kx + b(k\neq0)$经过点$C(1,0)$，且把$\triangle AOB$分成两部分.
（1）若$\triangle AOB$被分成的两部分面积相等，求$k$和$b$的值；
（2）若$\triangle AOB$被分成的两部分面积比为$1:5$，求$k$和$b$的值.
　　　　　　　　　　　

答案： 解：
(1) 依题意得 $A(2,0)$，$B(0,2)$. $\because\triangle AOB$ 被分成的两部分面积相等，$\therefore C$ 是 $OA$ 的中点，$\therefore S_{\triangle OBC}=S_{\triangle CBA}$，$\because y = kx + b$ 经过 $C(1,0)$，$B(0,2)$，$\therefore\begin{cases}k + b = 0 \\ b = 2\end{cases}$，解得$\begin{cases}b = 2 \\ k = -2\end{cases}$.
(2) 设 $y = kx + b$ 与 $OB$ 交于 $M(0,h)$，分 $\triangle AOB$ 的面积比为 $1:5$，得 $S_{\triangle OMC}=\frac{1}{6}S_{\triangle OBA}$. 则 $\frac{1}{2}\times1\times h=\frac{1}{6}\times\frac{1}{2}\times2\times2$，$\therefore h=\frac{2}{3}$，$\therefore M(0,\frac{2}{3})$. 经过 $M$ 点作直线 $MN// OA$，交 $AB$ 于 $N(a,\frac{2}{3})$，则 $S_{\triangle OMC}=S_{\triangle CAN}$. $\because N(a,\frac{2}{3})$ 在直线 $y = -x + 2$ 上，$\therefore a=\frac{4}{3}$，$\therefore N(\frac{4}{3},\frac{2}{3})$，$\because y = kx + b$ 经过 $M$，$C$ 或 $N$，$C$，解得$\begin{cases}k_{1}=-\frac{2}{3} \\ b_{1}=\frac{2}{3}\end{cases}$ 或 $\begin{cases}k_{2}=2 \\ b_{2}=-2\end{cases}$.

18. 小颖和小亮上山游玩，小颖乘坐缆车，小亮步行，两人相约在山顶的缆车终点会合. 已知小亮行走到缆车终点的路程是缆车到山顶的线路长的$2$倍. 小颖在小亮出发后$50\ min$才乘上缆车，缆车的平均速度为$180\ m/min$. 设小亮出发$x\ min$后行走的路程为$y\ m$，图中的折线表示小亮在整个行走过程中$y$与$x$的函数关系.
（1）小亮行走的总路程是__________$m$，他途中休息了__________$min$；
（2）①当$50\leqslant x\leqslant80$时，求$y$与$x$的函数关系式；
②当小颖到达缆车终点时，小亮离缆车终点的路程是多少？
　　　　　　　　

答案： 解：
(1) 3600 20
(2) ①当 $50\leqslant x\leqslant 80$ 时，设 $y$ 与 $x$ 的函数关系式为 $y = kx + b$，根据题意，当 $x = 50$ 时，$y = 1950$；当 $x = 80$ 时，$y = 3600$. $\therefore\begin{cases}50k + b = 1950 \\ 80k + b = 3600\end{cases}$，解得$\begin{cases}k = 55 \\ b = -800\end{cases}$. $\therefore$ 函数关系式为 $y = 55x - 800$. ②缆车到山顶的线路长为 $3600\div2 = 1800\ m$，缆车到达终点所需时间为 $1800\div180 = 10\ min$，小颖到达缆车终点时，小亮行走的时间为 $10 + 50 = 60\ min$，把 $x = 60$ 代入 $y = 55x - 800$，得 $y = 55\times60 - 800 = 2500$，$\therefore$ 当小颖到达缆车终点时，小亮离缆车终点的路程是 $3600 - 2500 = 1100\ m$.