《2025年赢在假期期末加寒假八年级数学沪科版合肥工业大学出版社》

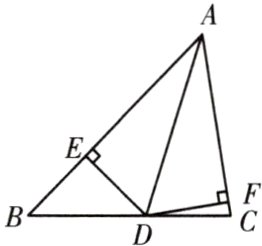
14. 如图所示，D为△ABC的边BC上的一点，过点D分别作DE⊥AB于点E，DF⊥AC于点F，且DE = DF.
求证：点E，F关于AD对称.
　　　　　　　　　　　

答案： 14.证明:连接EF;在Rt△AED和Rt△AFD中，$\begin{cases}DE = DF\\AD = AD\end{cases}$，
∴Rt△AED≌Rt△AFD(HL).
∴AE=AF,
∴点A在EF的垂直平分线上.又
∵DE=DF,
∴点D也在EF的垂直平分线上.
∴AD垂直平分EF.
∴点E,F关于AD对称.

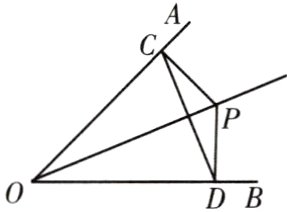
15. 如图，已知点P是∠AOB平分线上的一点，PC⊥OA，PD⊥OB，垂足分别为点C，D.
(1)∠PCD = ∠PDC成立吗？为什么？
(2)OP所在直线是线段CD的垂直平分线吗？为什么？
　　　　　　　　　　

答案： 15.解:
(1)成立，
∵OP是∠AOB的平分线，且PC⊥OA,PD⊥OB,
∴PC=PD,
∴∠PCD=∠PDC;　　
(2)是,在Rt△POC 和Rt△POD中，
∵PC=PD,OP=OP,
∴Rt△POC≌Rt△POD,
∴OC=OD.由PC=PD,OC=OD,可知点O,P都是线段CD的垂直平分线上的点，所以OP所在直线是线段CD的垂直平分线.

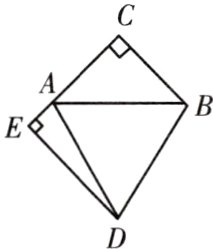
16. 如图所示，在△ABC中，∠ACB = 90°，AC = BC，D为△ABC外一点，且AD = BD，DE⊥AC交CA的延长线于点E. 试探求ED，AE和BC之间有何数量关系.
　　　　　　　　　　　　

答案：
16.如图所示，连接CD,交AB于点H.
∵AC=BC,
∴点C在AB的垂直平分线上.同理，点D也在AB的垂直平分线上,
∴CD即为AB的垂直平分线.
∵AC=
　　　　　　　　　　　　　　　　　
BC,∠ACB=90°,
∴∠ECD=45°.又
∵DE⊥CE,
∴∠EDC=45°,
∴EC=ED.而EC =AE+AC=AE+BC,
∴ED=BC+AE.

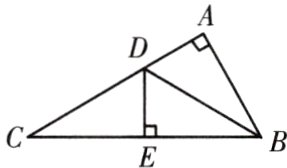
17. 如图所示，∠A = 90°，E为BC上的一点，点A和点E关于BD对称，点B和点C关于DE对称. 求∠ABC和∠C的度数.
　　　　　　　　　　

答案： 17.解:连接AE.
∵点A和点E关于BD对称,
∴BD是AE的垂直平分线.
∴BA=BE,DA=DE.又
∵DB=DB,
∴△DAB ≌△DEB.
∴∠ABD=∠EBD.
∵点B和点C关于DE 对称，
∴DE是BC的垂直平分线，
∴DC=DB,CE=BE.又
∵DE=DE,
∴△DCE≌△DBE;
∴∠C=∠EBD.
∴∠C=∠EBD=∠ABD.
∵∠C+∠EBD+∠ABD=90°,
∴∠C=30°,∠ABC=60°.