《2025年赢在假期期末加寒假八年级数学沪科版合肥工业大学出版社》

10. 若点$A(m - 1,2m)$在函数$y = 3x + 2$的图象上，则点$A$的坐标为__________.

答案： (0,2)

11. 一次函数图象与直线$y = 2x + 6$平行，且过点$(-1,1)$，则这个函数的解析式为________.

答案： $y = 2x + 3$

12. 小明放学后步行回家，他离家的路程$s$（$m$）与步行时间$t$（$min$）的函数图象如图所示，则他步行回家的平均速度是_______$m/min$.
　　　　　

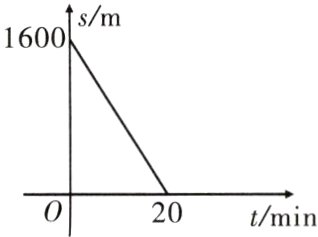
答案： 80

13. 已知一次函数$y=(a + 3)x+(b - 2)$.
（1）当$a$为何值时，$y$随$x$的增大而减小？
（2）当$a$，$b$为何值时，图象与$y$轴的交点在$x$轴上方？
（3）当$a$，$b$为何值时，图象经过第一、三、四象限？

答案： 解：
(1) 由一次函数的性质可知，当 $a + 3 ＜ 0$，即 $a ＜ -3$ 时，$y$ 随 $x$ 的增大而减小.
(2) 由题意得，$\begin{cases}a + 3 \neq 0 \\ b - 2 ＞ 0\end{cases}$，解得$\begin{cases}a \neq -3 \\ b ＞ 2\end{cases}$. $\therefore$ 当 $a \neq -3$ 且 $b ＞ 2$ 时，图象与 $y$ 轴的交点在 $x$ 轴上方.
(3) $\because$ 图象经过第一、三、四象限，$\therefore\begin{cases}a + 3 ＞ 0 \\ b - 2 ＜ 0\end{cases}$，$\therefore\begin{cases}a ＞ -3 \\ b ＜ 2\end{cases}$. 即当 $a ＞ -3$ 且 $b ＜ 2$ 时，图象经过第一、三、四象限.

14. 已知直线$y = kx + b$与$y$轴交于正半轴，且函数值$y$随$x$的增大而减小，则直线$y = bx + k$不经过第几象限？

答案： 解：因为直线 $y = kx + b$ 与 $y$ 轴交于正半轴，所以 $b ＞ 0$，所以直线 $y = bx + k$ 经过第一、三象限. 因为函数值 $y$ 随 $x$ 的增大而减小，所以 $k ＜ 0$，所以直线 $y = bx + k$ 与 $y$ 轴交于负半轴. 综上，直线 $y = bx + k$ 不经过第二象限.

15. 已知一次函数$y = kx + b$的图象经过$M(0,2)$，$N(1,3)$两点.
（1）求$k$，$b$的值；
（2）若一次函数$y = kx + b$的图象与$x$轴的交点为$A(a,0)$，求$a$的值.

答案： 解：
(1) 由题意，得$\begin{cases}b = 2 \\ k + b = 3\end{cases}$，解得$\begin{cases}k = 1 \\ b = 2\end{cases}$. $\therefore k$，$b$ 的值分别是 1 和 2；
(2) 由
(1)得 $y = x + 2$，$\therefore$ 当 $y = 0$ 时，$x = -2$，即 $a = -2$.

16. $A$，$B$两城相距$600\ km$，甲、乙两车同时从$A$城出发驶向$B$城，甲车到达$B$城后立即返回. 下图是它们离$A$城的距离$y$（$km$）与行驶时间$x$（$h$）之间的函数图象.
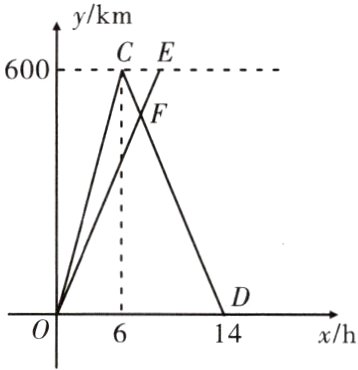
（1）求甲车行驶过程中$y$与$x$之间的函数解析式，并写出自变量$x$的取值范围；
（2）当它们行驶了$7\ h$时两车相遇，求乙车的速度.
　　　　　　　　

答案： 解：
(1) ①当 $0\leqslant x ＜ 6$ 时，$y = 100x$；②当 $6\leqslant x\leqslant 14$ 时，设 $y = kx + b$，$\because$ 图象过 $(6,600)$，$(14,0)$ 两点，$\therefore\begin{cases}6k + b = 600 \\ 14k + b = 0\end{cases}$，解得$\begin{cases}k = -75 \\ b = 1050\end{cases}$. $\therefore y = -75x + 1050$. $\therefore y =\begin{cases}100x(0\leqslant x ＜ 6) \\ -75x + 1050(6\leqslant x\leqslant 14)\end{cases}$.
(2) 当 $x = 7$ 时，$y = -75\times7 + 1050 = 525$，$v_{乙}=\frac{525}{7}=75\ km/h$.