《2025年赢在假期期末加寒假八年级数学沪科版合肥工业大学出版社》

6. 利用尺规作图法作出线段的垂直平分线.
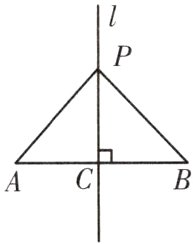
根据两点确定一条直线，只要找出到这条线段的两个端点距离相等的两个点，过这两个点作直线就能得到这条线段的垂直平分线.
如图所示，直线l是线段AB的垂直平分线，P为l上一点，则PA = PB；反过来，如果PA = PB，则点P在线段AB的垂直平分线上.

答案：

7. 线段垂直平分线的性质定理：线段垂直平分线上的点到______________相等.

答案：

7.线段两端

的距离

8. 线段垂直平分线的判定定理：到线段两端距离相等的点在线段的__________上.

答案：

8.垂直平分线

9. 三角形三边的垂直平分线相交于一点，这点到三角形______的距离相等.

答案：

9.三个顶点

例题 (1)如图(a)所示，已知线段AB，l为线段AB的垂直平分线，垂足为C，P为l上的任一点，求证：PA = PB.
(2)如图(b)所示，已知线段AB，PA = PB，求证：点P在线段AB的垂直平分线上.

证明 (1)∵l为线段AB的垂直平分线，∴AC = BC，且∠PCA = ∠PCB = 90°. 又∵PC为公共边，∴△PCA≌△PCB(SAS)，PA = PB. (2)过点P作PC⊥AB，垂足为C，如图所示(c). ∵PA = PB，PC = PC，且∠PCA = ∠PCB = 90°，∴Rt△PCA≌Rt△PCB(HL)，∴C为线段AB的中点. 又∵PC⊥AB，∴PC在AB的垂直平分线上. ∴点P在线段AB的垂直平分线上.

答案：

跟踪训练 如图所示，在△ABC中，D为BC上一点，且BC = BD + AD，则点D在线段__________的垂直平分线上.
[答案]　AC

答案：

10. 等腰三角形的性质
(1)定理1：等腰三角形的两底角相等(等边对等角).
(2)定理2：等腰三角形顶角的平分线______底边.
(3)等腰三角形的顶角平分线、底边上的中线和底边上的高“三线合一”.
等腰三角形“三线合一”性质的作用：可以证明角相等、线段相等或线段垂直，即等腰三角形顶角的平分线、底边上的中线、底边上的高，三者中只要满足其中一个，就可以求出其他两个.

答案：

10.
(2)垂直平分

11. 等腰三角形判定定理：有两个角相等的三角形是等腰三角形，简称“____________”.

答案： 11.等角对等边

12. 等边三角形的性质定理和判定定理
(1)性质定理：等边三角形三个内角相等，每一个内角都等于______.
(2)判定定理：①三个角都相等的三角形是等边三角形.
②有一个角是60°的______三角形是等边三角形.

答案： 12.
(1)60°
(2)②等腰