《2025年赢在假期期末加寒假八年级数学沪科版合肥工业大学出版社》

11. 如图所示，在△ABC中，∠C = 90°，AD平分∠BAC，CD = 3 cm，AB = 10 cm，则S△ABD = ____________.
　　

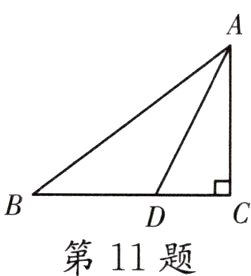
答案： $15\ cm^{2}$

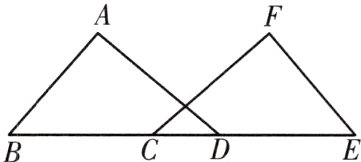
12. 如图，在△ABD和△FEC中，点B，C，D，E在同一直线上，且AB = FE，BC = DE，∠B = ∠E.
求证：∠ADB = ∠FCE.
　　　　　　　　　

答案： 证明：$\because BC = DE$，$\therefore BC + CD = DE + CD$，$\therefore BD = CE$. 又$\because AB = FE$，$\angle B=\angle E$，$\therefore \triangle ABD\cong \triangle FEC$，$\therefore \angle ADB = \angle FCE$.

13. 如图所示，某湖湖岸有A，B两棵大树，想在两棵大树间架一条电话线路. 为了计算两棵大树能承受的压力，需测量出A，B之间的距离，但是A，B两点又不能直接到达. 你能用已学过的知识和方法设计测量方案，求出A，B两点间的距离吗？并说明理由.
　　　　　　　　　　　

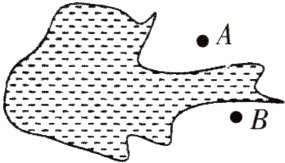
答案： 解：能利用“SAS”构造三角形全等的设计方案：先在地上取一个可以直接到达点A和点B的点C，连接BC并延长到E，使$CE = CB$；连接AC并延长到D，使$CD = CA$，连接DE并测量出它的长度，DE的长就是A，B两点之间的距离.

14. 如图所示，把长方形ABCD沿AE翻折，使点D落在BC边上的点F处. 如果∠BAF = 60°，那么∠DAE为多少度？
　　　　　　　　　　　

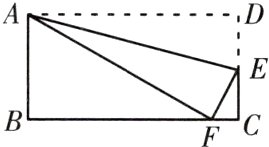
答案： 解：在长方形ABCD中，$\angle BAD = 90^{\circ}$，$\therefore \angle DAF=\angle BAD - \angle BAF = 30^{\circ}$. $\because \triangle AFE$是由$\triangle ADE$翻折得到的，$\therefore \triangle ADE\cong \triangle AFE$. $\therefore \angle DAE = \angle FAE$. $\therefore \angle DAE=\frac{1}{2}\angle DAF = 15^{\circ}$.

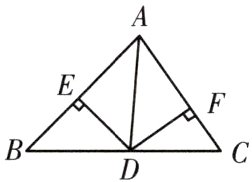
15. 如图所示，在△ABC中，AD是∠BAC的平分线，DE⊥AB于点E，DF⊥AC于点F.
求证：(1)AE = AF；
(2)AD平分∠EDF.
　　　　　　　　　　　

答案： 证明：
(1)$\because AD$平分$\angle BAC$，$\therefore \angle EAD = \angle FAD$. 又$\because DE\perp AB$，$DF\perp AC$，$\therefore \angle DEA=\angle DFA = 90^{\circ}$. 在$\triangle ADE$与$\triangle ADF$中，$\begin{cases}\angle EAD=\angle FAD,\\\angle DEA=\angle DFA,\\AD = AD,\end{cases}\therefore \triangle ADE\cong \triangle ADF$，$\therefore AE = AF$.
(2)由
(1)知$Rt\triangle ADE\cong Rt\triangle ADF$，$\therefore \angle ADE = \angle ADF$（全等三角形的对应角相等），即AD平分$\angle EDF$.

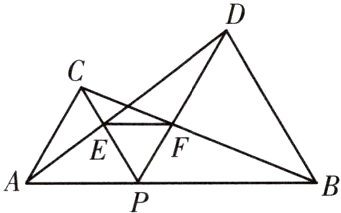
16. 如图所示，P是线段AB上一点，△APC和△BPD都是正三角形，AD与PC交于点E，BC与PD交于点F，连接EF，试探究△PEF的形状.
　　　　　　　　　　

答案： 等边三角形