《2025年优化探究同步导学案高中化学选择性必修1人教版》

1. (1) 已知下列反应的平衡常数：
${H_{2}(g) + S(s)\rightleftharpoons H_{2}S(g)}$ $K_{1}$
${S(s) + O_{2}(g)\rightleftharpoons SO_{2}(g)}$ $K_{2}$
则反应${H_{2}(g) + SO_{2}(g)\rightleftharpoons O_{2}(g) + H_{2}S(g)}$的平衡常数是$\frac{K_{1}}{K_{2}}$(用含$K_{1}$、$K_{2}$的式子表示)。
(2) 对于${N_{2}O_{4}(g)\rightleftharpoons 2NO_{2}(g)}$ $K=\frac{c_{ 平}^{2}({NO_{2}})}{c_{ 平}({N_{2}O_{4}})}$，列出下列反应的平衡常数表达式，并用$K$表示出来。
$\frac{1}{2}{N_{2}O_{4}(g)\rightleftharpoons NO_{2}(g)}$ $K' = $$\frac{c_{平}(NO_{2})}{c_{平}(N_{2}O_{4})}=\sqrt{K}$$$。
$2{NO_{2}(g)\rightleftharpoons N_{2}O_{4}(g)}$ $K'' = $$\frac{c_{平}(N_{2}O_{4})}{c_{平}^{2}(NO_{2})}=\frac{1}{K}$$$。

答案：
(1)$\frac{K_{1}}{K_{2}}$
(2)$\frac{c_{平}(NO_{2})}{c_{平}(N_{2}O_{4})}=\sqrt{K}$ $\frac{c_{平}(N_{2}O_{4})}{c_{平}^{2}(NO_{2})}=\frac{1}{K}$

2. 在一定体积的密闭容器中进行化学反应：${CO_{2}(g) + H_{2}(g)\rightleftharpoons CO(g) + H_{2}O(g)}$ $\Delta H$，其化学平衡常数和温度的关系如表所示：

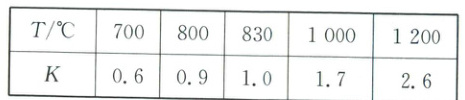
回答下列问题：
(1) 该反应的化学平衡常数表达式为$K = $$\frac{c_{平}(CO) · c_{平}(H_{2}O)}{c_{平}(CO_{2}) · c_{平}(H_{2})}$，$\Delta H$ ____(填“$＞$”“$=$”或“$＜$”)0。
(2) 某温度下，该反应的平衡浓度符合$c_{ 平}({CO_{2}})· c_{ 平}({H_{2}})=c_{ 平}(CO)· c_{ 平}({H_{2}O})$，试判断此时的温度为830$^{\circ} C$。
(3) 在$800^{\circ} C$时，发生上述反应，某一时刻测得容器内各物质的浓度分别为$c({CO_{2}})=2\ mol· L^{-1}$，$c({H_{2}})=1.5\ mol· L^{-1}$，$c(CO)=1\ mol· L^{-1}$，$c({H_{2}O})=3\ mol· L^{-1}$，则反应逆向(填“正向”或“逆向”)进行。

答案：
(1)$\frac{c_{平}(CO) · c_{平}(H_{2}O)}{c_{平}(CO_{2}) · c_{平}(H_{2})}$＞
(2)830
(3)逆向
解析：
(1)升高温度，平衡常数增大，说明$\Delta H＞0$。
(2)当$c_{平}(CO_{2}) · c_{平}(H_{2}) = c_{平}(CO) · c_{平}(H_{2}O)$时，即$K = 1$，对应表中温度为$830^{\circ}C$。
(3)$800^{\circ}C$时，$Q = \frac{c(CO) · c(H_{2}O)}{c(CO_{2}) · c(H_{2})} = \frac{1mol· L^{-1} × 3mol· L^{-1}}{2mol· L^{-1} × 1.5mol· L^{-1}} = 1＞K = 0.9$，$Q＞K$，反应逆向进行。

1. 平衡转化率的概念
(1) 定义
对于反应：$a A+b B\rightleftharpoons c C+d D$，反应物$ A$的平衡转化率可以表示为$\alpha( A) = $$\frac{初始时A的物质的量 - 平衡时A的物质的量}{初始时A的物质的量} × 100\%$$$。
特别提醒 对于溶液体系和恒容的气态反应体系，可以用物质的量浓度进行计算。即对于反应$a A+b B\rightleftharpoons c C+d D$，反应物$ A$的平衡转化率$\alpha( A)=\frac{ A的初始浓度- A的平衡浓度}{ A的初始浓度}×100\%$。
(2) 意义
平衡常数和平衡转化率都可以表示可逆反应的限度，平衡常数基于反应，而平衡转化率基于反应物，因此平衡转化率能更直观地反映某一反应物转化的程度。
(3) 影响因素与变化规律
分析依据：若分析某反应物$ A$的平衡转化率的变化情况，若初始时$ A$的量一定，则转化的$ A$的量越大，其平衡转化率越大，反之越小；若初始时$ A$的量和转化的$ A$的量都增大(或减小)，则要看增大(或减小)的程度。
① 温度和压强：改变温度或压强，使平衡正向移动，则所有反应物的平衡转化率均增大。
② 恒温恒容条件下：a. 两种或两种以上的气态物质参与反应，增加一种物质的量，其他反应物的平衡转化率增大，该物质的平衡转化率减小；若成比例(已知平衡的投料比)地增加每一种气体反应物的量，相当于增大压强，反之，相当于减小压强；b. 只有一种气体反应物，增加该气体的量，相当于增大压强，反之，相当于减小压强。

答案：
(1)$\frac{初始时A的物质的量 - 平衡时A的物质的量}{初始时A的物质的量} × 100\%$
(2)反应 反应物
(3)增大

2. 平衡常数及平衡转化率的相关计算
可逆反应：$m A( g) + n B( g)\rightleftharpoons p C( g) + q D( g)$，在体积为$V\ L$的恒容密闭容器中，反应物$ A$、$ B$的初始加入量分别为$a\ mol$、$b\ mol$，达到化学平衡时，设$ A$物质转化的物质的量为$mx\ mol$。
(1) 计算模型——“三段式”法
$\begin{aligned}m A( g) + n B( g) &\rightleftharpoons p C( g) + q D( g) \\起始量/ mol & a b 0 0 \\转化量/ mol & mx \ nx \ px \ qx \\平衡量/ mol & a - mx b - nx \ px \ qx \\\end{aligned}$
(2) 思维模型——三步骤
① 巧设未知量，列全三段式：找已知量，设转化量(若能由已知量列三段式就不必设量)。
② 抽提关键量，找准关系式：依据转化量之比等于化学计量数之比或关键量列等式关系。
③ 解答设问题，求解问题项：根据求解量，计算问题项。
(3) 常常计算的物理量及其公式
① 平衡常数$K = \frac{\left( \frac{px}{V} \right)^{p} · \left( \frac{qx}{V} \right)^{q}}{\left( \frac{a - mx}{V} \right)^{m} · \left( \frac{b - nx}{V} \right)^{n}}$。
② 平衡时$ A$的物质的量浓度：$c_{ 平}( A) = \frac{a - mx}{V}\ mol· L^{-1}$。
③ 平衡时$ A$的平衡转化率：$\alpha = \frac{mx}{a} × 100\%$，$ A$、$ B$的平衡转化率之比为$\alpha( A) : \alpha( B) = \frac{mx}{a} : \frac{nx}{b}$。
④ 平衡时$ A$的体积分数：$\varphi( A) = \frac{a - mx}{a - mx + b - nx + px + qx} × 100\%$。
⑤ 平衡时和开始时的压强之比：$\frac{p( 平)}{p( 始)} = \frac{a - mx + b - nx + px + qx}{a + b}$。
⑥ 生成物产率$= \frac{ 该物质的实际产量}{ 该物质的理论产量} × 100\%$。

答案： 化学计量数