2025年优化探究同步导学案高中化学选择性必修1人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年优化探究同步导学案高中化学选择性必修1人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
1. 已知$\triangle(g) + H_2(g) = CH_3CH_2CH_3(g) \Delta H_1 = -157 kJ · mol^{-1}$。已知$\triangle(g)$的燃烧热$\Delta H_2 = -2 092 kJ · mol^{-1}$,$CH_3CH_2CH_3(g)$的燃烧热$\Delta H_3 = -2 220 kJ · mol^{-1}$,1 mol 液态水转变为气态水的焓变为$\Delta H_4 = +44 kJ · mol^{-1}$。则 2 mol 氢气完全燃烧生成气态水的$\Delta H$(kJ·mol⁻¹)为 (
A.$-658 kJ · mol^{-1}$
B.$-482 kJ · mol^{-1}$
C.$-329 kJ · mol^{-1}$
D.$-285 kJ · mol^{-1}$
B
)A.$-658 kJ · mol^{-1}$
B.$-482 kJ · mol^{-1}$
C.$-329 kJ · mol^{-1}$
D.$-285 kJ · mol^{-1}$
答案:
1.$B$ ①$\Delta(g)+H_2(g)\xlongequal\ CH_3CH_2CH_3(g)\ \Delta H_1 = -157\ kJ· mol^{-1}$,由题意知②$\Delta(g)+\frac{9}{2}O_2(g)\xlongequal\ 3CO_2(g)+3H_2O(l)\ \Delta H_2 = -2092\ kJ· mol^{-1}$,③$CH_3CH_2CH_3(g)+5O_2(g)\xlongequal\ 3CO_2(g)+4H_2O(l)\ \Delta H_3 = -2220\ kJ· mol^{-1}$,④$H_2O(l)\xlongequal\ H_2O(g)\ \Delta H_4 = +44\ kJ· mol^{-1}$,根据盖斯定律,由①$-$②$+$③$+$④得$H_2(g)+\frac{1}{2}O_2(g)\xlongequal\ H_2O(g)\ \Delta H'=\Delta H_1-\Delta H_2+\Delta H_3+\Delta H_4 = -241\ kJ· mol^{-1}$,则$2\ mol$氢气完全燃烧生成气态水的热化学方程式为$2H_2(g)+O_2(g)\xlongequal\ 2H_2O(g)\ \Delta H = -482\ kJ· mol^{-1}$,B项正确。
2. 已知冶炼铁的过程中发生如下反应:
①$Fe_2O_3(s) + 3CO(g) = 2Fe(s) + 3CO_2(g) \Delta H_1 = -25 kJ · mol^{-1}$;
②$3Fe_2O_3(s) + CO(g) = 2Fe_3O_4(s) + CO_2(g) \Delta H_2 = -47 kJ · mol^{-1}$;
③$Fe_3O_4(s) + CO(g) = 3FeO(s) + CO_2(g) \Delta H_3 = +19 kJ · mol^{-1}$。
写出$FeO(s)$被 CO 还原成 Fe 和$CO_2$的热化学方程式:
①$Fe_2O_3(s) + 3CO(g) = 2Fe(s) + 3CO_2(g) \Delta H_1 = -25 kJ · mol^{-1}$;
②$3Fe_2O_3(s) + CO(g) = 2Fe_3O_4(s) + CO_2(g) \Delta H_2 = -47 kJ · mol^{-1}$;
③$Fe_3O_4(s) + CO(g) = 3FeO(s) + CO_2(g) \Delta H_3 = +19 kJ · mol^{-1}$。
写出$FeO(s)$被 CO 还原成 Fe 和$CO_2$的热化学方程式:
$FeO(s)+CO(g)\xlongequal\ Fe(s)+CO_2(g)\ \Delta H = -11\ kJ· mol^{-1}$
。
答案:
2.答案$FeO(s)+CO(g)\xlongequal\ Fe(s)+CO_2(g)\ \Delta H = -11\ kJ· mol^{-1}$
解析:依据盖斯定律:一个化学反应,不管是一步完成的还是分几步完成的,其反应热是相同的。$FeO$与$CO$反应生成$Fe$和$CO_2$的化学方程式:$FeO(s)+CO(g)\xlongequal\ Fe(s)+CO_2(g)$ ④,由盖斯定律可得,$\frac{1}{6}×[3×$①$-(2×$③$+$②$)]=$④,可得该反应的反应热:$\Delta H=\frac{1}{6}[3\Delta H_1-(2\Delta H_3+\Delta H_2)]=\frac{1}{6}\{3×(-25)-[2×(+19)+(-47)]\}\ kJ· mol^{-1}=-11\ kJ· mol^{-1}$。
解析:依据盖斯定律:一个化学反应,不管是一步完成的还是分几步完成的,其反应热是相同的。$FeO$与$CO$反应生成$Fe$和$CO_2$的化学方程式:$FeO(s)+CO(g)\xlongequal\ Fe(s)+CO_2(g)$ ④,由盖斯定律可得,$\frac{1}{6}×[3×$①$-(2×$③$+$②$)]=$④,可得该反应的反应热:$\Delta H=\frac{1}{6}[3\Delta H_1-(2\Delta H_3+\Delta H_2)]=\frac{1}{6}\{3×(-25)-[2×(+19)+(-47)]\}\ kJ· mol^{-1}=-11\ kJ· mol^{-1}$。
[例 1] $ A(g)+B(g)=C(g) \Delta H_{1}<0 $
$ A(g)+B(g)=C(l) \Delta H_{2}<0 $
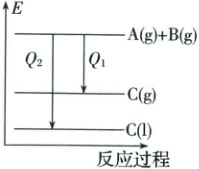
由物质的能量(E)的大小知热量:$ Q_{1} $
$ A(g)+B(g)=C(l) \Delta H_{2}<0 $

由物质的能量(E)的大小知热量:$ Q_{1} $
<
(填“>”“<”或“=”,下同)$ Q_{2} $,反应为放热反应,所以 $ \Delta H_{1} $>
$ \Delta H_{2} $。
答案:
[例1] < >
[例 2] 如 $ S(g)+O_{2}(g)=SO_{2}(g) \Delta H_{1} $
$ S(s)+O_{2}(g)=SO_{2}(g) \Delta H_{2} $
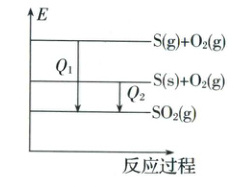
由物质的能量(E)的大小知热量:$ Q_{1} $
$ S(s)+O_{2}(g)=SO_{2}(g) \Delta H_{2} $

由物质的能量(E)的大小知热量:$ Q_{1} $
>
$ Q_{2} $,反应为放热反应,则 $ \Delta H_{1} $<
$ \Delta H_{2} $。
答案:
[例2] > <
[例 3] 已知:$ C(s, 金刚石)=C(s, 石墨) \Delta H=-1.9 \mathrm{~kJ} · \mathrm{mol}^{-1} $
$ C(s, 金刚石)+O_{2}(g)=CO_{2}(g) \Delta H_{1} $
$ C(s, 石墨)+O_{2}(g)=CO_{2}(g) \Delta H_{2} $
根据上述反应所得出的结论正确的是(
A.$ \Delta H_{1}=\Delta H_{2} $
B.$ \Delta H_{1}>\Delta H_{2} $
C.$ \Delta H_{1}<\Delta H_{2} $
D.金刚石比石墨稳定
$ C(s, 金刚石)+O_{2}(g)=CO_{2}(g) \Delta H_{1} $
$ C(s, 石墨)+O_{2}(g)=CO_{2}(g) \Delta H_{2} $
根据上述反应所得出的结论正确的是(
C
)A.$ \Delta H_{1}=\Delta H_{2} $
B.$ \Delta H_{1}>\Delta H_{2} $
C.$ \Delta H_{1}<\Delta H_{2} $
D.金刚石比石墨稳定
答案:
[例3] C 已知:$\mathrm{C(s,金刚石)══C(s,石墨)}$ $\Delta H = -1.9\ kJ· mol^{-1}$,则等量的金刚石和石墨,金刚石的能量高,燃烧放出的热量多,则$\Delta H_1 < \Delta H_2 < 0$,能量越高越不稳定,则石墨比金刚石稳定。
查看更多完整答案,请扫码查看


