《2026年一本密卷高考数学》

1. (2025·河北省张家口三模)已知 $ \sin \left( \alpha + \frac{\pi}{6} \right) = -\frac{1}{12} $，则 $ \sin \left( 2\alpha - \frac{\pi}{6} \right) = $ (D)

A.$ \frac{12}{13} $
B.$ -\frac{12}{13} $
C.$ \frac{71}{72} $
D.$ -\frac{71}{72} $

答案： 1.D 因为 $\sin \left(\alpha+\frac{\pi}{6}\right)=-\frac{1}{12}$，则
$\sin \left(2\alpha-\frac{\pi}{6}\right)=-\sin \left(\frac{\pi}{6}-2\alpha\right)$
$=-\sin \left[\frac{\pi}{2}-2\left(\alpha+\frac{\pi}{6}\right)\right]=-\cos \left[2\left(\alpha+\frac{\pi}{6}\right)\right]$
$=-\left[1-2\sin^2 \left(\alpha+\frac{\pi}{6}\right)\right]=2× \left(-\frac{1}{12}\right)^2-1$
$=-\frac{71}{72}$. 故选 D.

2. (2025·河北石家庄三模)将函数 $ f(x) = \sin \left( 2x + \frac{\pi}{3} \right) + 3 $ 的图象向右平移 $ \frac{\pi}{12} $ 个单位长度，得到函数 $ g(x) $ 的图象，则函数 $ g(x) $ 图象的一个对称中心是 (A)

A.$ \left( -\frac{\pi}{12}, 3 \right) $
B.$ \left( -\frac{\pi}{12}, 0 \right) $
C.$ \left( \frac{\pi}{6}, 3 \right) $
D.$ \left( \frac{\pi}{6}, 0 \right) $

答案： 2.A 由题知 $g(x)=f\left(x-\frac{\pi}{12}\right)=\sin \left[2\left(x-\frac{\pi}{12}\right)+\frac{\pi}{3}\right]+3=\sin \left(2x+\frac{\pi}{6}\right)+3$. 令 $2x+\frac{\pi}{6}=k\pi,k\in \mathbb{Z}$，
解得 $x=-\frac{\pi}{12}+\frac{k\pi}{2},k\in \mathbb{Z}$，$\therefore$ 函数 $g(x)$ 图象的对称
中心为 $\left(-\frac{\pi}{12}+\frac{k\pi}{2},3\right),k\in \mathbb{Z}$，$\therefore$ 当 $k = 0$ 时，
$\left(-\frac{\pi}{12},3\right)$ 为函数 $g(x)$ 图象的一个对称中心. 故
选 A.

3. (2025·辽宁沈阳三模)已知函数 $ f(x) = 2\sin \left( \omega x - \frac{\pi}{3} \right)(\omega ＞ 0) $ 在区间 $ \left( \frac{\pi}{3}, \pi \right) $ 上有且仅有一个零点，当 $ \omega $ 最大时，$ f(x) $ 的图象的一条对称轴方程为 (B)

A.$ x = \frac{17}{12}\pi $
B.$ x = \frac{17}{14}\pi $
C.$ x = \frac{23}{10}\pi $
D.$ x = \frac{23}{18}\pi $

答案： 3.B 当 $\frac{\pi}{3}＜x＜\pi$ 时，且 $\omega＞0$，$\frac{\pi}{3}\omega-\frac{\pi}{3}＜\omega x-\frac{\pi}{3}＜\pi\omega-\frac{\pi}{3}$，由 $f(x)=0$ 可得 $\sin \left(\omega x-\frac{\pi}{3}\right)=0$，所以
$k\pi\leq \frac{\pi}{3}\omega-\frac{\pi}{3}＜(k + 1)\pi$，
$(k + 1)\pi＜\pi\omega-\frac{\pi}{3}\leq(k + 2)\pi$，
解得$\begin{cases}3k + 1\leq\omega＜3k + 4\frac{3k}{}+\frac{4}{3}＜\omega\leq k+\frac{7}{3}\end{cases}$
若 $\omega$ 无解，则 $3k + 4\leq k+\frac{4}{3}$ 或 $k+\frac{7}{3}＜3k + 1$，
解得 $k\leq-\frac{4}{3}$ 或 $k＞\frac{2}{3}$，
由于 $\omega＞0$ 且 $\omega$ 存在，故 $k = 0$ 或 $k=-1$，
即$\begin{cases}1\leq\omega＜4\\-2\leq\omega＜1\end{cases}$或$\begin{cases}\frac{4}{3}＜\omega\leq\frac{7}{3}\frac{1}{3}＜\omega\leq\frac{4}{3}\end{cases}$，
则有 $\frac{4}{3}＜\omega\leq\frac{7}{3}$ 或 $\frac{1}{3}＜\omega＜1$，
故 $\omega$ 的最大值为 $\frac{7}{3}$，
此时 $f(x)=2\sin \left(\frac{7x}{3}-\frac{\pi}{3}\right)$，
由 $\frac{7x}{3}-\frac{\pi}{3}=\frac{\pi}{2}+m\pi(m\in \mathbb{Z})$ 可得 $x=\frac{5\pi}{14}+\frac{3m}{7}\pi(m\in \mathbb{Z})$，当 $m = 2$ 时，函数 $f(x)$ 的一条对称轴方程为
$x=\frac{17}{14}\pi$. 故选 B.

4. (2025·浙江省金华市义乌市三模)在 $ \triangle ABC $ 中，角 $ A、B、C $ 所对的边分别为 $ a、b、c $，已知 $ A = \frac{\pi}{6} $，$ a = \sqrt{2} $，$ b = 2 $，则下列结论一定正确的是 (D)

A.$ B ＜ \frac{\pi}{3} $
B.$ B ＞ \frac{\pi}{2} $
C.$ c ＞ 2 $
D.$ c ＜ 3 $

答案： 4.D 由正弦定理可得 $\frac{a}{\sin A}=\frac{b}{\sin B}\Rightarrow\sin B=\frac{b\sin A}{a}$
$=\frac{2×\frac{1}{2}}{\sqrt{2}}=\frac{\sqrt{2}}{2}$，由于 $B\in\left(0,\frac{5\pi}{6}\right)$，故 $B=\frac{\pi}{4}$ 或 $B=\frac{3\pi}{4}$，故 A、B错误，若 $B=\frac{\pi}{4}$ 时，则 $C=\pi - A - B=\pi$
$-\frac{\pi}{6}-\frac{\pi}{4}=\frac{5\pi}{12}$，此时 $c=\frac{a\sin C}{\sin A}=\frac{\sqrt{2}\sin \left(\frac{\pi}{6}+\frac{\pi}{4}\right)}{\frac{1}{2}}$
$=\frac{\sqrt{2}\left(\sin\frac{\pi}{6}\cos\frac{\pi}{4}+\cos\frac{\pi}{6}\sin\frac{\pi}{4}\right)}{}=\frac{}{}2\sqrt{2}×\frac{\sqrt{2 + \sqrt{6}}}{4}=1+\sqrt{3}＜3$，若 $B=\frac{3\pi}{4}$ 时，则 $C=\pi - A - B=\pi-\frac{\pi}{6}-\frac{3\pi}{4}=\frac{\pi}{12}$，此时 $C$ 为三角形中最小的内角，故 $c＜a=\sqrt{2}$，故 C错误，D正确. 故选 D.

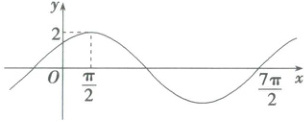
5. (2025·广东省广州市天河区三模)已知函数 $ f(x) = 2\sin(\omega x + \varphi) \left( \omega ＞ 0, |\varphi| ＜ \frac{\pi}{2} \right) $ 的部分图象如图所示，若 $ A，B，C $ 是直线 $ y = m(m ＞ 0) $ 与函数 $ f(x) $ 图象的从左至右相邻的三个交点，且 $ |AB| = \frac{1}{3}|BC| $，则 $ m = $ (B)


A.1
B.$ \sqrt{2} $
C.$ \sqrt{3} $
D.$ \frac{4}{3} $

答案： 5.B 由题意可得 $\frac{3T}{4}-\frac{7\pi}{2}-\frac{\pi}{2}=3\pi$，所以最小正周期
$T = 4\pi$，所以 $\frac{2\pi}{\omega}=4\pi$，解得 $\omega=\frac{1}{2}$，所以 $f(x)=2\sin \left(\frac{1}{2}x+\varphi\right)$，由图象过点 $\left(\frac{\pi}{2},2\right)$，所以 $2\sin \left(\frac{\pi}{4}+\varphi\right)=2$，所以 $\sin \left(\frac{\pi}{4}+\varphi\right)=1$，所以 $\frac{\pi}{4}+\varphi=\frac{\pi}{2}+2k\pi,k\in \mathbb{Z}$，所以 $=\frac{\pi}{4}+2k\pi,k\in \mathbb{Z}$，又 $|\varphi|＜\frac{\pi}{2}$，所以 $\varphi=\frac{\pi}{4}$，所以 $f(x)=2\sin \left(\frac{1}{2}x+\frac{\pi}{4}\right)$，因为 $A,B,C$ 是
直线 $y = m(m＞0)$ 与函数 $f(x)$ 图象的从左至右相
邻的三个交点，且 $|AB|=\frac{1}{3}|BC|$，所以 $\frac{1}{2}|AB|+\frac{1}{2}|BC|=2\pi$，所以 $4|AB|=4\pi$，所以 $|AB|=\pi$，所
以 $\frac{1}{2}|AB|=\frac{\pi}{2}$，所以 $m = 2\sin \left[\frac{1}{2}\left(\frac{\pi}{2}+\frac{\pi}{2}\right)+\frac{\pi}{4}\right]$
$=2\cos \frac{\pi}{4}=\sqrt{2}$. 故选 B.

6. (2025·湖南省郴州市三模)已知 $ \alpha + \beta = \frac{5\pi}{6} $，$ \sin 2\alpha + \sin 2\beta = \frac{2}{3} $，则 $ \cos 2\alpha + \cos 2\beta = $ (C)

A.$ \pm \frac{2\sqrt{3}}{3} $
B.$ \frac{2}{3} $
C.$ -\frac{2\sqrt{3}}{3} $
D.$ \frac{2\sqrt{3}}{3} $

答案： 6.C $\sin 2\alpha+\sin 2\beta=\sin [(\alpha+\beta)+(\alpha-\beta)]+\sin [(\alpha+\beta)-(\alpha-\beta)]=2\sin (\alpha+\beta)\cos (\alpha-\beta)$
$=\frac{2}{3}$，
由 $\alpha+\beta=\frac{5\pi}{6}$，得 $\sin (\alpha+\beta)=\frac{1}{2}$，则 $\cos (\alpha-\beta)$
$=\frac{2}{3}$，
$\cos 2\alpha+\cos 2\beta=\cos [(\alpha+\beta)+(\alpha-\beta)]+\cos [(\alpha+\beta)-(\alpha-\beta)]$
$=2\cos (\alpha+\beta)\cos (\alpha-\beta)=2×\left(-\frac{\sqrt{3}}{2}\right)×\frac{2}{3}=-\frac{2\sqrt{3}}{3}$. 故选 C.

7. (2025·湖北武汉市武昌区三模)已知函数 $ f(x) = \sin \left( 2x - \frac{\pi}{6} \right) $，则 (ABC)

A.$ f(x) $ 的最小正周期为 $ \pi $
B.$ f(x) $ 在区间 $ \left( 0, \frac{\pi}{6} \right) $ 上单调递增
C.$ f(x) $ 的一个对称中心为 $ \left( \frac{7\pi}{12}, 0 \right) $
D.$ f(x) $ 图象上所有的点向左平移 $ \frac{\pi}{6} $ 个单位长度后关于 $ y $ 轴对称

答案： 7.ABC 对于 A，由周期公式可得最小正周期为 $\frac{2\pi}{\omega}=\pi$，A正确；对于 B，由 $x\in\left(0,\frac{\pi}{6}\right)$，则 $2x-\frac{\pi}{6}\in\left(-\frac{\pi}{6},\frac{\pi}{6}\right)$，由正弦函数的单调性可知 $f(x)$ 在区间
$\left(0,\frac{\pi}{6}\right)$ 上单调递增，B正确；对于 C，当 $x=\frac{7\pi}{12}$ 时，
$f\left(\frac{7\pi}{12}\right)=\sin \left(2×\frac{7\pi}{12}-\frac{\pi}{6}\right)=0$，C 正确；对于 D，
$f(x)$ 图象上所有的点向左平移 $\frac{\pi}{6}$ 个单位长度后，
得到 $g(x)=\sin \left[2\left(x+\frac{\pi}{6}\right)-\frac{\pi}{6}\right]=\sin \left(2x+\frac{\pi}{6}\right)$，
显然图象关于 $y$ 轴不对称，D错误. 故选 ABC.