2026年一本密卷高考数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年一本密卷高考数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 已知集合 $ A = \{ x | y = \sqrt{x - 2} \} $, $ B = \{ x | x^2 - 4x + 3 \leq 0 \} $, 则 $ A \cup B = $ (
A.$ \{ x | 2 \leq x \leq 3 \} $
B.$ \{ x | x \geq 2 \} $
C.$ \{ x | x \leq 1 $, 或 $ x \geq 2 \} $
D.$ \{ x | x \geq 1 \} $
D
)A.$ \{ x | 2 \leq x \leq 3 \} $
B.$ \{ x | x \geq 2 \} $
C.$ \{ x | x \leq 1 $, 或 $ x \geq 2 \} $
D.$ \{ x | x \geq 1 \} $
答案:
1.D 因为集合$A=\{x\mid y=\sqrt{x - 2}\}=\{x\mid x\geq2\}$,集合$B=\{x\mid x^2 - 4x + 3\leq0\}=\{x\mid1\leq x\leq3\}$,所以$A\cup B=\{x\mid x\geq1\}$.故选D.
2. 复数 $ z $ 满足 $ (1 - i)z = |2i| $, 则复数 $ z $ 的虚部为 (
A.$ -1 $
B.$ -\frac{1}{2} $
C.$ \frac{1}{2} $
D.$ 1 $
D
)A.$ -1 $
B.$ -\frac{1}{2} $
C.$ \frac{1}{2} $
D.$ 1 $
答案:
2.D 因为$(1 - i)z = |2i|$,即$(1 - i)z = 2$,所以$z = \frac{2}{1 - i}=\frac{2(1 + i)}{(1 - i)(1 + i)} = 1 + i$,所以复数$z$的虚部为1.故选D.
3. 已知向量 $ \boldsymbol{a}, \boldsymbol{b} $ 满足 $ |\boldsymbol{a}| = 2 $, $ |\boldsymbol{a} - 2\boldsymbol{b}| = 2 $, 且 $ (\boldsymbol{a} - \boldsymbol{b}) \perp \boldsymbol{a} $, 则 $ |\boldsymbol{b}| = $ (
A.$ 2 $
B.$ \sqrt{2} $
C.$ 1 $
D.$ \frac{\sqrt{2}}{2} $
A
)A.$ 2 $
B.$ \sqrt{2} $
C.$ 1 $
D.$ \frac{\sqrt{2}}{2} $
答案:
3.A 因为$|a| = 2$,$|a - 2b| = 2$,且$(a - b)\perp a$,所以$\begin{cases}(a - 2b)^2 = a^2 - 4a· b + 4b^2 = 4\\(a - b)· a = a^2 - a· b = 0\end{cases}$,即$a· b = |a|^2 = 4$,$2^2 - 4×4 + 4|b|^2 = 4$,解得$|b| = 2$(负值已舍去).故选A.
4. 若 $ \alpha \in (\pi, \frac{3\pi}{2}) $, $ \tan \alpha = \frac{\cos \alpha}{\sin \alpha - 1} $, 则 $ \sin \alpha = $ (
A.$ -\frac{1}{2} $
B.$ -\frac{\sqrt{2}}{2} $
C.$ -\frac{\sqrt{3}}{2} $
D.$ -\frac{1}{3} $
A
)A.$ -\frac{1}{2} $
B.$ -\frac{\sqrt{2}}{2} $
C.$ -\frac{\sqrt{3}}{2} $
D.$ -\frac{1}{3} $
答案:
4.A 由$\tan\alpha = \frac{\cos\alpha}{\sin\alpha - 1}=\frac{\sin\alpha}{\cos\alpha}$,得$\cos^2\alpha = \sin^2\alpha - \sin\alpha$,$\because\sin^2\alpha + \cos^2\alpha = 1$,$\therefore2\sin^2\alpha - \sin\alpha - 1 = 0$,即$(2\sin\alpha + 1)(\sin\alpha - 1) = 0$,解得$\sin\alpha = -\frac{1}{2}$或$\sin\alpha = 1$,$\because\alpha\in(\pi,\frac{3\pi}{2})$,$\therefore - 1 < \sin\alpha < 0$,$\therefore\sin\alpha = -\frac{1}{2}$.故选A.
5. 在正三棱台 $ ABC - A_1B_1C_1 $ 中, $ AB = 4 $, $ A_1B_1 = 2 $, $ A_1A $ 与平面 $ ABC $ 所成角为 $ \frac{\pi}{4} $, 则该三棱台的体积为 (
A.$ \frac{52}{3} $
B.$ \frac{28}{3} $
C.$ \frac{14}{3} $
D.$ \frac{7}{3} $
C
)A.$ \frac{52}{3} $
B.$ \frac{28}{3} $
C.$ \frac{14}{3} $
D.$ \frac{7}{3} $
答案:
5.C 由题设,将棱台补全为正棱锥$P - ABC$,如图,且$\triangle A_1B_1C_1$,$\triangle ABC$均为正三角形,其中$O$为底面$ABC$中心,连接$PO$,则$PO\perp$面$ABC$,而$AO\subset$面$ABC$,即$PO\perp AO$,所以$A_1A$与平面$ABC$所成角为$\angle PAO = \frac{\pi}{4}$,而$AB = 4$,则$AO = \frac{2}{3}× AB·\sin60° = \frac{4\sqrt{3}}{3}$,所以$PO = AO = \frac{4\sqrt{3}}{3}$,令$P - A_1B_1C_1$的高为$h$,结合棱台的结构特征,知$\frac{h}{PO}=\frac{A_1B_1}{AB}\Rightarrow h=\frac{PO}{2}=\frac{2\sqrt{3}}{3}$,所以棱台体积$V = V_{P - ABC}-V_{P - A_1B_1C_1}=\frac{1}{3}×\frac{\sqrt{3}}{4}×(4^2×\frac{4\sqrt{3}}{3}-2^2×\frac{2\sqrt{3}}{3})=\frac{14}{3}$.
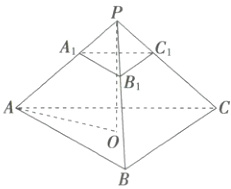
故选C.
5.C 由题设,将棱台补全为正棱锥$P - ABC$,如图,且$\triangle A_1B_1C_1$,$\triangle ABC$均为正三角形,其中$O$为底面$ABC$中心,连接$PO$,则$PO\perp$面$ABC$,而$AO\subset$面$ABC$,即$PO\perp AO$,所以$A_1A$与平面$ABC$所成角为$\angle PAO = \frac{\pi}{4}$,而$AB = 4$,则$AO = \frac{2}{3}× AB·\sin60° = \frac{4\sqrt{3}}{3}$,所以$PO = AO = \frac{4\sqrt{3}}{3}$,令$P - A_1B_1C_1$的高为$h$,结合棱台的结构特征,知$\frac{h}{PO}=\frac{A_1B_1}{AB}\Rightarrow h=\frac{PO}{2}=\frac{2\sqrt{3}}{3}$,所以棱台体积$V = V_{P - ABC}-V_{P - A_1B_1C_1}=\frac{1}{3}×\frac{\sqrt{3}}{4}×(4^2×\frac{4\sqrt{3}}{3}-2^2×\frac{2\sqrt{3}}{3})=\frac{14}{3}$.

故选C.
6. 已知函数 $ f(x) = \begin{cases} e^{-x}, & x < 2, \\ (x - 1)(x - 2)^2 + a, & x \geq 2 \end{cases} $ 存在最小值, 则实数 $ a $ 的取值范围是 (
A.$ (-\infty, -e^2] $
B.$ (-e^2, +\infty) $
C.$ (-\infty, e^{-2}] $
D.$ (e^{-2}, +\infty) $
C
)A.$ (-\infty, -e^2] $
B.$ (-e^2, +\infty) $
C.$ (-\infty, e^{-2}] $
D.$ (e^{-2}, +\infty) $
答案:
6.C 当$x < 2$时,函数$f(x) = e^{-x}$单调递减,$f(x) > e^{-2}$无最小值;当$x\geq2$时,函数$f(x) = (x - 1)(x - 2)^2 + a$,当$x\geq2$时,函数$f'(x) = (x - 2)^2 + 2(x - 2)(x - 1) = (x - 2)(3x - 4)$,所以$x\in[2,+\infty)$,$f'(x)\geq0$,$f(x)$单调递增,当$x = 2$时,$f(x)_{\min} = (2 - 1)(2 - 2)^2 + a = a$,要使函数$f(x)$存在最小值,即$a\leq e^{-2}$.故选C.
7. 将函数 $ g(x) = \cos (\omega x + \frac{\pi}{12}) (\omega \in \mathbf{N}^*) $ 的图象上所有点的横坐标变为原来的 $ \frac{1}{2} $, 纵坐标变为原来的 $ 2 $ 倍, 得到函数 $ f(x) $ 的图象, 若 $ f(x) $ 在 $ (0, \frac{\pi}{2}) $ 上只有一个极大值点, 则 $ \omega $ 的最大值为 (
A.$ 2 $
B.$ 3 $
C.$ 4 $
D.$ 5 $
B
)A.$ 2 $
B.$ 3 $
C.$ 4 $
D.$ 5 $
答案:
7.B 由题可知$f(x) = 2\cos(2\omega x + \frac{\pi}{12})(\omega\in N^*)$,当$0 < x < \frac{\pi}{2}$时,$\frac{\pi}{12} < 2\omega x + \frac{\pi}{12} < \omega\pi + \frac{\pi}{12}$,若$f(x)$在$(0,\frac{\pi}{2})$上只有一个极大值点,则由$y = 2\cos x$的图象可得$2\pi < \omega\pi + \frac{\pi}{12}\leq4\pi$,解得$\frac{23}{12} < \omega\leq\frac{47}{12}$,因为$\omega\in N^*$,所以$\omega$的最大值为3.
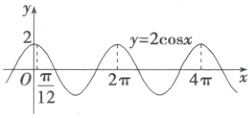
故选B.
7.B 由题可知$f(x) = 2\cos(2\omega x + \frac{\pi}{12})(\omega\in N^*)$,当$0 < x < \frac{\pi}{2}$时,$\frac{\pi}{12} < 2\omega x + \frac{\pi}{12} < \omega\pi + \frac{\pi}{12}$,若$f(x)$在$(0,\frac{\pi}{2})$上只有一个极大值点,则由$y = 2\cos x$的图象可得$2\pi < \omega\pi + \frac{\pi}{12}\leq4\pi$,解得$\frac{23}{12} < \omega\leq\frac{47}{12}$,因为$\omega\in N^*$,所以$\omega$的最大值为3.

故选B.
8. 已知函数 $ f(x) $ 的定义域为 $ \mathbf{R} $, 函数 $ F(x) = f(1 + x) - (1 + x) $ 为偶函数, 函数 $ G(x) = f(2 + 3x) - 1 $ 为奇函数, 则下列说法错误的是 (
A.函数 $ f(x) $ 的一个对称中心为 $ (2, 1) $
B.$ f(0) = -1 $
C.函数 $ f(x) $ 为周期函数, 且一个周期为 $ 4 $
D.$ f(1) + f(2) + f(3) + f(4) = 6 $
C
)A.函数 $ f(x) $ 的一个对称中心为 $ (2, 1) $
B.$ f(0) = -1 $
C.函数 $ f(x) $ 为周期函数, 且一个周期为 $ 4 $
D.$ f(1) + f(2) + f(3) + f(4) = 6 $
答案:
8.C 对于A,因为$G(x) = f(2 + 3x) - 1$为奇函数,所以$G(-x) = -G(x)$,即$f(2 - 3x) - 1 = -[f(2 + 3x) - 1]$,所以$f(2 - 3x) + f(2 + 3x) = 2$,所以$f(2 - x) + f(2 + x) = 2$,所以函数$f(x)$的图象关于点$(2,1)$对称,所以A正确.对于B,在$f(2 - x) + f(2 + x) = 2$中,令$x = 0$,得$2f(2) = 2$,得$f(2) = 1$,因为函数$F(x) = f(1 + x) - (1 + x)$为偶函数,所以$F(-x) = F(x)$,所以$f(1 - x) - (1 - x) = f(1 + x) - (1 + x)$,所以$f(1 + x) - f(1 - x) = 2x$,令$x = 1$,则$f(2) - f(0) = 2$,所以$1 - f(0) = 2$,得$f(0) = -1$,所以B正确.对于C,因为函数$f(x)$的图象关于点$(2,1)$对称,$f(0) = -1$,所以$f(4) = 3$,所以$f(0)\neq f(4)$,所以4不是$f(x)$的周期,所以C错误.对于D,在$f(2 - x) + f(2 + x) = 2$中令$x = 1$,则$f(1) + f(3) = 2$,令$x = 2$,则$f(0) + f(4) = 2$,因为$f(0) = -1$,所以$f(4) = 3$,因为$f(2) = 1$,所以$f(1) + f(2) + f(3) + f(4) = 6$,所以D正确.故选C.
查看更多完整答案,请扫码查看


