2026年一本密卷高考数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年一本密卷高考数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
6. 已知数列 $ \{a_{n}\} $ 的前 $ n $ 项和为 $ S_{n} $,$ a_{n}\neq 0 $,$ a_{n}a_{n + 2} = a_{n + 1}^{2} $ 且 $ a_{6}a_{9} = 2a_{4}a_{10} $,则 $ \frac{S_{4}}{S_{8}} = $(
A.$ \frac{1}{17} $
B.$ \frac{16}{17} $
C.$ \frac{17}{16} $
D.17
A
)A.$ \frac{1}{17} $
B.$ \frac{16}{17} $
C.$ \frac{17}{16} $
D.17
答案:
6. A 因为$a_n a_{n + 2} = a_{n + 1}^2$,且$a_n \neq 0$,
所以$\frac{a_{n + 2}}{a_{n + 1}} = \frac{a_{n + 1}}{a_n} = ·s = \frac{a_2}{a_1}$,
所以$\{a_n\}$为等比数列。
因为$a_6 a_9 = 2a_4 a_{10}$,
所以$a_5 a_{10} = 2a_4 a_{10}$,
因为$a_{10} \neq 0$,所以$a_5 = 2a_4$,
即$\{a_n\}$的公比$q = \frac{a_5}{a_4} = 2$。
方法一:所以$\frac{S_4}{S_8} = \frac{S_4}{(1 + q^4)S_4} = \frac{1}{1 + q^4} = \frac{1}{1 + 2^4} = \frac{1}{17}$。故选A。
方法二:所以$\frac{S_4}{S_8} = \frac{\frac{a_1(1 - q^4)}{1 - q}}{\frac{a_1(1 - q^8)}{1 - q}} = \frac{1}{1 + q^4} = \frac{1}{1 + 2^4} = \frac{1}{17}$。
故选A。
所以$\frac{a_{n + 2}}{a_{n + 1}} = \frac{a_{n + 1}}{a_n} = ·s = \frac{a_2}{a_1}$,
所以$\{a_n\}$为等比数列。
因为$a_6 a_9 = 2a_4 a_{10}$,
所以$a_5 a_{10} = 2a_4 a_{10}$,
因为$a_{10} \neq 0$,所以$a_5 = 2a_4$,
即$\{a_n\}$的公比$q = \frac{a_5}{a_4} = 2$。
方法一:所以$\frac{S_4}{S_8} = \frac{S_4}{(1 + q^4)S_4} = \frac{1}{1 + q^4} = \frac{1}{1 + 2^4} = \frac{1}{17}$。故选A。
方法二:所以$\frac{S_4}{S_8} = \frac{\frac{a_1(1 - q^4)}{1 - q}}{\frac{a_1(1 - q^8)}{1 - q}} = \frac{1}{1 + q^4} = \frac{1}{1 + 2^4} = \frac{1}{17}$。
故选A。
7. (多选)设 $ m $,$ n $ 是两条不同的直线,$ \alpha $,$ \beta $ 是两个不同的平面.下列各选项中,满足“$ q $ 的充分条件是 $ p $”的有(
A.$ p:m// n,m\perp\alpha $. $ q:n\perp\alpha $
B.$ p:m// n,m//\alpha $. $ q:n//\alpha $
C.$ p:m\subset\alpha,n\subset\beta,m//\beta,n//\alpha $. $ q:\alpha//\beta $
D.$ p:m//\alpha,m\perp\beta $. $ q:\alpha\perp\beta $
AD
)A.$ p:m// n,m\perp\alpha $. $ q:n\perp\alpha $
B.$ p:m// n,m//\alpha $. $ q:n//\alpha $
C.$ p:m\subset\alpha,n\subset\beta,m//\beta,n//\alpha $. $ q:\alpha//\beta $
D.$ p:m//\alpha,m\perp\beta $. $ q:\alpha\perp\beta $
答案:
7. AD “$q$的充分条件是$p$”即“$p\Rightarrow q$”,则只需判断$p\Rightarrow q$是否为真命题即可。
对于A,两条平行直线中的一条直线垂直于一个平面,则另一条直线也垂直于这个平面,所以$p\Rightarrow q$。
对于B,如图,在长方体$ABCD - A_1B_1C_1D_1$中,令$m$为$A_1B_1$,$n$为$AB$,平面$\alpha$为平面$ABCD$,则$A_1B_1// AB$,$A_1B_1//$平面$ABCD$,但$AB\subset$平面$ABCD$,所以$p\nRightarrow q$。
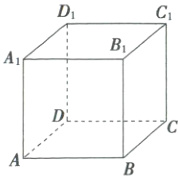
对于C,令$m$为$AA_1$,$n$为$CC_1$,平面$\alpha$为平面$ABB_1A_1$,平面$\beta$为平面$BCC_1B_1$,则$AA_1\subset$平面$ABB_1A_1$,$AA_1//$平面$BCC_1B_1$,$CC_1\subset$平面$BCC_1B_1$,$CC_1//$平面$ABB_1A_1$,但平面$ABB_1A_1$与平面$BCC_1B_1$相交,所以$p\nRightarrow q$。
对于D,设$m\subset$平面$\gamma$,$\alpha\cap\gamma = l$,因为$m//\alpha$,所以$m// l$。
又$m\perp\beta$,所以$l\perp\beta$。又$l\subset\alpha$,所以$\alpha\perp\beta$,$p\Rightarrow q$。故选AD。
7. AD “$q$的充分条件是$p$”即“$p\Rightarrow q$”,则只需判断$p\Rightarrow q$是否为真命题即可。
对于A,两条平行直线中的一条直线垂直于一个平面,则另一条直线也垂直于这个平面,所以$p\Rightarrow q$。
对于B,如图,在长方体$ABCD - A_1B_1C_1D_1$中,令$m$为$A_1B_1$,$n$为$AB$,平面$\alpha$为平面$ABCD$,则$A_1B_1// AB$,$A_1B_1//$平面$ABCD$,但$AB\subset$平面$ABCD$,所以$p\nRightarrow q$。

对于C,令$m$为$AA_1$,$n$为$CC_1$,平面$\alpha$为平面$ABB_1A_1$,平面$\beta$为平面$BCC_1B_1$,则$AA_1\subset$平面$ABB_1A_1$,$AA_1//$平面$BCC_1B_1$,$CC_1\subset$平面$BCC_1B_1$,$CC_1//$平面$ABB_1A_1$,但平面$ABB_1A_1$与平面$BCC_1B_1$相交,所以$p\nRightarrow q$。
对于D,设$m\subset$平面$\gamma$,$\alpha\cap\gamma = l$,因为$m//\alpha$,所以$m// l$。
又$m\perp\beta$,所以$l\perp\beta$。又$l\subset\alpha$,所以$\alpha\perp\beta$,$p\Rightarrow q$。故选AD。
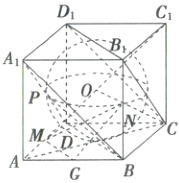
8. (多选)如图,在正方体 $ ABCD - A_{1}B_{1}C_{1}D_{1} $ 中,$ \overrightarrow{A_{1}P} = \lambda\overrightarrow{A_{1}D}(0\leqslant\lambda\leqslant 1) $,$ \overrightarrow{AG} = \mu\overrightarrow{AB}(0\leqslant\mu\leqslant 1) $,点 $ M $,$ N $ 分别为 $ AD $,$ BB_{1} $ 的中点,且该正方体的内切球为球 $ O $,则下列说法正确的有(

A.$ AC_{1}\perp BP $
B.平面 $ A_{1}PB// $ 平面 $ B_{1}D_{1}C $
C.存在 $ \mu $,使得 $ OC\perp $ 平面 $ MNG $
D.若球 $ O $ 的半径 $ R = 1 $,则过直线 $ MN $ 的平面截球 $ O $ 所得的所有截面圆中,半径最小的圆的面积为 $ \frac{\pi}{3} $
ABC
)
A.$ AC_{1}\perp BP $
B.平面 $ A_{1}PB// $ 平面 $ B_{1}D_{1}C $
C.存在 $ \mu $,使得 $ OC\perp $ 平面 $ MNG $
D.若球 $ O $ 的半径 $ R = 1 $,则过直线 $ MN $ 的平面截球 $ O $ 所得的所有截面圆中,半径最小的圆的面积为 $ \frac{\pi}{3} $
答案:
8. ABC 对于A,如图,连接$AC$,$BD$,则$AC\perp BD$,易知$CC_1\perp$平面$ABCD$,$BD\subset$平面$ABCD$,所以$CC_1\perp BD$,又$CC_1\cap AC = C$,$CC_1$,$AC\subset$平面$AC_1C$,所以$BD\perp$平面$AC_1C$,而$AC_1\subset$平面$AC_1C$,所以$BD\perp AC_1$。
同理可得$BA_1\perp AC_1$,又$BD\cap BA_1 = B$,$BD$,$BA_1\subset$平面$A_1BD$,所以$AC_1\perp$平面$A_1BD$,
又$BP\subset$平面$A_1BD$,所以$AC_1\perp BP$,A正确。
对于B,在正方体中,有平面$A_1BD//$平面$B_1D_1C$,
即平面$A_1PB//$平面$B_1D_1C$,B正确。
对于C,当$\mu = \frac{1}{2}$时,点$G$为$AB$的中点,所以$MG\perp AC$,又$OC$在平面$ABCD$上的射影落在$AC$上,所以$MG\perp OC$,同理$GN\perp OC$。又$MG\cap GN = G$,$MG$,$GN\subset$平面$MNG$,所以$OC\perp$平面$MNG$,C正确。
对于D,因为球$O$的半径$R = 1$,所以正方体的棱长为$2$,设点$Q$是线段$MN$的中点,连接$OQ$,$OM$(图略),易知$M$,$N$到点$O$的距离相等,所以$OQ\perp MN$,由勾股定理易知$MN = \sqrt{1^2 + 2^2 + 1^2} = \sqrt{6}$,$OM = \sqrt{2}$,
则球心$O$到$MN$的距离为$OQ = \sqrt{OM^2 - QM^2} = \sqrt{(\sqrt{2})^2 - (\frac{\sqrt{6}}{2})^2} = \frac{\sqrt{2}}{2}$,
所以$MN$被球$O$截得的弦长$l = 2\sqrt{R^2 - OQ^2} = 2\sqrt{1 - (\frac{\sqrt{2}}{2})^2} = \sqrt{2}$,
所以半径最小的截面圆的半径$r = \frac{l}{2} = \frac{\sqrt{2}}{2}$,面积$S = \pi r^2 = \frac{1}{2}\pi$,D错误。
故选ABC。
8. ABC 对于A,如图,连接$AC$,$BD$,则$AC\perp BD$,易知$CC_1\perp$平面$ABCD$,$BD\subset$平面$ABCD$,所以$CC_1\perp BD$,又$CC_1\cap AC = C$,$CC_1$,$AC\subset$平面$AC_1C$,所以$BD\perp$平面$AC_1C$,而$AC_1\subset$平面$AC_1C$,所以$BD\perp AC_1$。
同理可得$BA_1\perp AC_1$,又$BD\cap BA_1 = B$,$BD$,$BA_1\subset$平面$A_1BD$,所以$AC_1\perp$平面$A_1BD$,
又$BP\subset$平面$A_1BD$,所以$AC_1\perp BP$,A正确。
对于B,在正方体中,有平面$A_1BD//$平面$B_1D_1C$,
即平面$A_1PB//$平面$B_1D_1C$,B正确。
对于C,当$\mu = \frac{1}{2}$时,点$G$为$AB$的中点,所以$MG\perp AC$,又$OC$在平面$ABCD$上的射影落在$AC$上,所以$MG\perp OC$,同理$GN\perp OC$。又$MG\cap GN = G$,$MG$,$GN\subset$平面$MNG$,所以$OC\perp$平面$MNG$,C正确。
对于D,因为球$O$的半径$R = 1$,所以正方体的棱长为$2$,设点$Q$是线段$MN$的中点,连接$OQ$,$OM$(图略),易知$M$,$N$到点$O$的距离相等,所以$OQ\perp MN$,由勾股定理易知$MN = \sqrt{1^2 + 2^2 + 1^2} = \sqrt{6}$,$OM = \sqrt{2}$,
则球心$O$到$MN$的距离为$OQ = \sqrt{OM^2 - QM^2} = \sqrt{(\sqrt{2})^2 - (\frac{\sqrt{6}}{2})^2} = \frac{\sqrt{2}}{2}$,
所以$MN$被球$O$截得的弦长$l = 2\sqrt{R^2 - OQ^2} = 2\sqrt{1 - (\frac{\sqrt{2}}{2})^2} = \sqrt{2}$,
所以半径最小的截面圆的半径$r = \frac{l}{2} = \frac{\sqrt{2}}{2}$,面积$S = \pi r^2 = \frac{1}{2}\pi$,D错误。

故选ABC。
查看更多完整答案,请扫码查看


