2026年一本密卷高考数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年一本密卷高考数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
4. (2025·四川省成都市三模)已知某地社交媒体用户的日活跃时长 $X$(单位:小时)服从正态分布 $N(2.4, 0.7^{2})$,则下面描述不正确的是(
A.$E(X)=2.4$,$D(X)=0.7^{2}$
B.若 $P(X\leqslant 1)=P(X\geqslant b)$,则 $b = 3$
C.$P(X\leqslant 0.3)+P(X\geqslant 4.5)<P(0.3<X<4.5)$
D.$P(|X - 2|\leqslant 0.7)\geqslant P(|X - 3|\leqslant 0.7)$
B
)A.$E(X)=2.4$,$D(X)=0.7^{2}$
B.若 $P(X\leqslant 1)=P(X\geqslant b)$,则 $b = 3$
C.$P(X\leqslant 0.3)+P(X\geqslant 4.5)<P(0.3<X<4.5)$
D.$P(|X - 2|\leqslant 0.7)\geqslant P(|X - 3|\leqslant 0.7)$
答案:
4.B 因为$X$(单位:小时)服从正态分布$N(2.4,0.7^2)$,$\mu = 2.4$,$\sigma = 0.7$,根据正态分布知识,$E(X) = 2.4$,$D(X) = 0.7^2$,A正确;
若$P(X \leq 1) = P(X \geq b)$,则$\frac{1 + b}{2} = 2.4$,得$b = 3.8$,B错误;
$P(X \leq 0.3) + P(X \geq 4.5) = P(X \leq 2.4 - 3×0.7) + P(X \geq 2.4 + 3×0.7)$,根据$3\sigma$原则,可得$P(X \leq 0.3) + P(X \geq 4.5) < P(0.3 < X < 4.5)$,C正确;
$P(|X - 2| \leq 0.7) = P(1.3 \leq X \leq 2.7) = P(1.3 \leq X \leq 2.3) + P(2.3 < X \leq 2.7)$,$P(|X - 3| \leq 0.7) = P(2.3 \leq X \leq 3.7) = P(2.3 \leq X < 2.7) + P(2.7 \leq X \leq 3.7)$,由对称性可知$P(1.3 \leq X \leq 2.3) > P(2.7 \leq X \leq 3.7)$,所以$P(|X - 2| \leq 0.7) \geq P(|X - 3| \leq 0.7)$,D正确。故选B。
若$P(X \leq 1) = P(X \geq b)$,则$\frac{1 + b}{2} = 2.4$,得$b = 3.8$,B错误;
$P(X \leq 0.3) + P(X \geq 4.5) = P(X \leq 2.4 - 3×0.7) + P(X \geq 2.4 + 3×0.7)$,根据$3\sigma$原则,可得$P(X \leq 0.3) + P(X \geq 4.5) < P(0.3 < X < 4.5)$,C正确;
$P(|X - 2| \leq 0.7) = P(1.3 \leq X \leq 2.7) = P(1.3 \leq X \leq 2.3) + P(2.3 < X \leq 2.7)$,$P(|X - 3| \leq 0.7) = P(2.3 \leq X \leq 3.7) = P(2.3 \leq X < 2.7) + P(2.7 \leq X \leq 3.7)$,由对称性可知$P(1.3 \leq X \leq 2.3) > P(2.7 \leq X \leq 3.7)$,所以$P(|X - 2| \leq 0.7) \geq P(|X - 3| \leq 0.7)$,D正确。故选B。
5. (2025·山东省枣庄市三模)已知 $A$,$B$ 为随机事件,且 $P(A)=0.5$,$P(B)=0.4$,则下列结论错误的是(
A.若 $A$,$B$ 互斥,则 $P(A\cup B)=0.9$
B.若 $A$,$B$ 相互独立,则 $P(A\overline{B})=0.2$
C.若 $A$,$B$ 相互独立,则 $P(A\cup B)=0.7$
D.若 $P(B|A)=0.5$,则 $P(B|\overline{A})=0.3$
B
)A.若 $A$,$B$ 互斥,则 $P(A\cup B)=0.9$
B.若 $A$,$B$ 相互独立,则 $P(A\overline{B})=0.2$
C.若 $A$,$B$ 相互独立,则 $P(A\cup B)=0.7$
D.若 $P(B|A)=0.5$,则 $P(B|\overline{A})=0.3$
答案:
5.B 对于A选项,若A,B互斥,根据互斥事件的概率加法公式$P(A \cup B) = P(A) + P(B)$。已知$P(A) = 0.5$,$P(B) = 0.4$,则$P(A \cup B) = 0.5 + 0.4 = 0.9$,所以A选项正确。
对于B选项,若A,B相互独立,则A与$\overline{B}$也相互独立。因为$P(\overline{B}) = 1 - P(B) = 1 - 0.4 = 0.6$,所以$P(A\overline{B}) = P(A)P(\overline{B}) = 0.5×0.6 = 0.3 \neq 0.2$,所以B选项错误。
对于C选项,若A,B相互独立,则$P(AB) = P(A)P(B) = 0.5×0.4 = 0.2$。根据概率的加法公式$P(A \cup B) = P(A) + P(B) - P(AB)$,将$P(A) = 0.5$,$P(B) = 0.4$,$P(AB) = 0.2$代入可得:$P(A \cup B) = 0.5 + 0.4 - 0.2 = 0.7$,所以C选项正确。
对于D选项,已知$P(B|A) = \frac{P(AB)}{P(A)} = 0.5$,$P(A) = 0.5$,则$P(AB) = 0.5×0.5 = 0.25$。$P(\overline{A}) = 1 - P(A) = 1 - 0.5 = 0.5$,$P(B\overline{A}) = P(B) - P(AB) = 0.4 - 0.25 = 0.15$。根据条件概率公式$P(B|\overline{A}) = \frac{P(B\overline{A})}{P(\overline{A})} = \frac{0.15}{0.5} = 0.3$,所以D选项正确。故选B。
对于B选项,若A,B相互独立,则A与$\overline{B}$也相互独立。因为$P(\overline{B}) = 1 - P(B) = 1 - 0.4 = 0.6$,所以$P(A\overline{B}) = P(A)P(\overline{B}) = 0.5×0.6 = 0.3 \neq 0.2$,所以B选项错误。
对于C选项,若A,B相互独立,则$P(AB) = P(A)P(B) = 0.5×0.4 = 0.2$。根据概率的加法公式$P(A \cup B) = P(A) + P(B) - P(AB)$,将$P(A) = 0.5$,$P(B) = 0.4$,$P(AB) = 0.2$代入可得:$P(A \cup B) = 0.5 + 0.4 - 0.2 = 0.7$,所以C选项正确。
对于D选项,已知$P(B|A) = \frac{P(AB)}{P(A)} = 0.5$,$P(A) = 0.5$,则$P(AB) = 0.5×0.5 = 0.25$。$P(\overline{A}) = 1 - P(A) = 1 - 0.5 = 0.5$,$P(B\overline{A}) = P(B) - P(AB) = 0.4 - 0.25 = 0.15$。根据条件概率公式$P(B|\overline{A}) = \frac{P(B\overline{A})}{P(\overline{A})} = \frac{0.15}{0.5} = 0.3$,所以D选项正确。故选B。
6. (2025·河南省焦作市三模)如图,一个圆形仓鼠笼被分为 $A$,$B$,$C$,$D$ 四个区域,相邻区域之间用通道相连,开始时将一只仓鼠放入 $A$ 区域,仓鼠每次随机选择一个通道进入相邻的区域,设经过 $n$ 次随机选择后仓鼠在 $A$ 区域的概率为 $x_{n}$,则下面描述不正确的是(
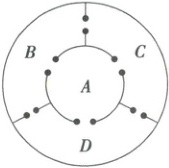
A.$x_{1}=0$
B.$x_{n + 1}^{2}=x_{n}x_{n + 2}$
C.$x_{2n + 1}>x_{2n - 1}$
D.$x_{2n - 1}+x_{2n}<\frac{1}{2}$
B
)
A.$x_{1}=0$
B.$x_{n + 1}^{2}=x_{n}x_{n + 2}$
C.$x_{2n + 1}>x_{2n - 1}$
D.$x_{2n - 1}+x_{2n}<\frac{1}{2}$
答案:
6.B 对于A,因为仓鼠一开始在A区域,经过1次选择后不可能在A区域,所以$x_1 = 0$,故A正确;
对于B,记仓鼠经过$n$次随机选择后在B,C,D区域的概率分别为$B_n$,$C_n$,$D_n$,则有$\begin{cases}x_n + B_n + C_n + D_n = 1\\x_{n + 1} = \frac{1}{3}B_n + \frac{1}{3}C_n + \frac{1}{3}D_n\end{cases}$,所以$x_{n + 1} = \frac{1}{3}(1 - x_n)$,进一步得$x_{n + 1} - \frac{1}{4} = - \frac{1}{3}(x_n - \frac{1}{4})$。因为$x_1 = 0$,所以$x_n - \frac{1}{4} = - \frac{1}{4} · (-\frac{1}{3})^{n - 1}$,所以$x_n = \frac{1}{4} - \frac{1}{4} · (-\frac{1}{3})^{n - 1}$,所以$\{x_n\}$不成等比数列,故B错误;
对于C,因为$x_{2n + 1} = \frac{1}{4} - \frac{1}{4} · (-\frac{1}{3})^{2n - 1} = \frac{1}{4} + \frac{1}{4} · (\frac{1}{3})^{2n - 1}$,$x_{2n - 1} = \frac{1}{4} - \frac{1}{4} · (-\frac{1}{3})^{2n - 2} = \frac{1}{4} - \frac{1}{4} · (\frac{1}{3})^{2n - 2}$,所以$x_{2n + 1} > x_{2n - 1}$,故C正确;
对于D,因为$x_{2n} = \frac{1}{4} - \frac{1}{4} · (-\frac{1}{3})^{2n - 1} = \frac{1}{4} + \frac{1}{4} · (\frac{1}{3})^{2n - 1}$,所以$x_{2n - 1} + x_{2n} = \frac{1}{2} + \frac{1}{4}[(\frac{1}{3})^{2n - 1} - (\frac{1}{3})^{2n - 2}] = \frac{1}{2} - \frac{1}{6} · (\frac{1}{3})^{2n - 2} < \frac{1}{2}$,故D正确。故选B。
对于B,记仓鼠经过$n$次随机选择后在B,C,D区域的概率分别为$B_n$,$C_n$,$D_n$,则有$\begin{cases}x_n + B_n + C_n + D_n = 1\\x_{n + 1} = \frac{1}{3}B_n + \frac{1}{3}C_n + \frac{1}{3}D_n\end{cases}$,所以$x_{n + 1} = \frac{1}{3}(1 - x_n)$,进一步得$x_{n + 1} - \frac{1}{4} = - \frac{1}{3}(x_n - \frac{1}{4})$。因为$x_1 = 0$,所以$x_n - \frac{1}{4} = - \frac{1}{4} · (-\frac{1}{3})^{n - 1}$,所以$x_n = \frac{1}{4} - \frac{1}{4} · (-\frac{1}{3})^{n - 1}$,所以$\{x_n\}$不成等比数列,故B错误;
对于C,因为$x_{2n + 1} = \frac{1}{4} - \frac{1}{4} · (-\frac{1}{3})^{2n - 1} = \frac{1}{4} + \frac{1}{4} · (\frac{1}{3})^{2n - 1}$,$x_{2n - 1} = \frac{1}{4} - \frac{1}{4} · (-\frac{1}{3})^{2n - 2} = \frac{1}{4} - \frac{1}{4} · (\frac{1}{3})^{2n - 2}$,所以$x_{2n + 1} > x_{2n - 1}$,故C正确;
对于D,因为$x_{2n} = \frac{1}{4} - \frac{1}{4} · (-\frac{1}{3})^{2n - 1} = \frac{1}{4} + \frac{1}{4} · (\frac{1}{3})^{2n - 1}$,所以$x_{2n - 1} + x_{2n} = \frac{1}{2} + \frac{1}{4}[(\frac{1}{3})^{2n - 1} - (\frac{1}{3})^{2n - 2}] = \frac{1}{2} - \frac{1}{6} · (\frac{1}{3})^{2n - 2} < \frac{1}{2}$,故D正确。故选B。
7. (2025·江西九江市三模)已知随机变量 $X$,$Y$,$X\sim B(10,p)$,$Y\sim N(4,4)$,则下列说法正确的是(
A.若 $P(X = 3)=P(X = 7)$,则 $p=\frac{1}{2}$
B.$D(X)>\frac{5}{2}$
C.$P(Y>4)>\frac{1}{2}$
D.$P(Y<2)=P(Y>6)$
AD
)A.若 $P(X = 3)=P(X = 7)$,则 $p=\frac{1}{2}$
B.$D(X)>\frac{5}{2}$
C.$P(Y>4)>\frac{1}{2}$
D.$P(Y<2)=P(Y>6)$
答案:
7.AD $P(X = 3) = C_{10}^3 p^3 (1 - p)^7$,$P(X = 7) = C_{10}^7 p^7 (1 - p)^3$,由$C_{10}^3 p^3 (1 - p)^7 = C_{10}^7 p^7 (1 - p)^3$,等式化简为$p^3 (1 - p)^7 = p^7 (1 - p)^3 \Rightarrow (1 - p)^4 = p^4 \Rightarrow p = \frac{1}{2}$,故A正确;
二项分布方差为$D(X) = 10p(1 - p)$,当$p = \frac{1}{2}$时,$D(X) = 10×\frac{1}{2}×\frac{1}{2} = 2.5$,此时$D(X) = \frac{5}{2}$。对于其他$p$,$D(X) < \frac{5}{2}$,故B错误;
$Y \sim N(4,4)$,均值$\mu = 4$,因此$P(Y > 4) = \frac{1}{2}$,故C错误;由正态分布的对称性,2和6关于$\mu = 4$对称,根据对称性,$P(Y < 2) = P(Y > 6)$,故D正确。故选AD。
二项分布方差为$D(X) = 10p(1 - p)$,当$p = \frac{1}{2}$时,$D(X) = 10×\frac{1}{2}×\frac{1}{2} = 2.5$,此时$D(X) = \frac{5}{2}$。对于其他$p$,$D(X) < \frac{5}{2}$,故B错误;
$Y \sim N(4,4)$,均值$\mu = 4$,因此$P(Y > 4) = \frac{1}{2}$,故C错误;由正态分布的对称性,2和6关于$\mu = 4$对称,根据对称性,$P(Y < 2) = P(Y > 6)$,故D正确。故选AD。
8. (2025·陕西省安康市三模)在平面直角坐标系上的一只蚂蚁从原点出发,每次随机地向上、下、左、右四个方向移动 1 个单位长度,移动 6 次,则(
A.蚂蚁始终未远离原点超过 1 个单位长度的概率是 $\frac{1}{64}$
B.蚂蚁移动到点 $(3,3)$ 的概率为 $\frac{5}{512}$
C.蚂蚁回到原点的概率为 $\frac{25}{256}$
D.蚂蚁移动到直线 $y = x$ 上的概率为 $\frac{5}{16}$
ACD
)A.蚂蚁始终未远离原点超过 1 个单位长度的概率是 $\frac{1}{64}$
B.蚂蚁移动到点 $(3,3)$ 的概率为 $\frac{5}{512}$
C.蚂蚁回到原点的概率为 $\frac{25}{256}$
D.蚂蚁移动到直线 $y = x$ 上的概率为 $\frac{5}{16}$
答案:
8.ACD 对于A,蚂蚁始终未远离原点超过1个单位长度,则每一步的位置只能是$(0,0)$或原点的上下左右四个点。最开始蚂蚁在原点,第一次移动有上下左右4种走法,第二次移动只能回到原点,即只有1种走法,同理,第三次移动有上下左右4种走法,第四次移动只能回到原点,即只有1种走法,第五次移动有上下左右4种走法,第六次移动只能回到原点,即只有1种走法,所以满足题意的共有$4×1×4×1×4×1 = 64$种路径。而移动6次,每次有4种走法,即总路径数为$4^6$,由古典概型可知蚂蚁始终未远离原点超过1个单位长度的概率为$\frac{64}{4^6} = \frac{1}{64}$,故A正确;
对于B,蚂蚁移动到点$(3,3)$,则需恰好右移3次,上移3次,路径数为$C_6^3 C_3^3 = 20$(种),所以蚂蚁移动到点$(3,3)$的概率为$\frac{20}{4^6} = \frac{5}{1024}$,故B错误;
对于C,要回到原点,则左右移动次数相等,均为$a$次;上下移动次数相等,均为$b$次,总次数满足$2a + 2b = 6$,即$a + b = 3$,可能的组合有:
①$a = 3$,$b = 0$,即左右都3次,路径数为$C_6^3 C_3^0 C_3^3 = 20$(种);
②$a = 2$,$b = 1$,即左右均2次,上下均1次,路径数为$C_6^4 C_4^2 C_2^2 = 180$(种);
③$a = 1$,$b = 2$,即左右均1次,上下均2次,路径数为$C_6^2 C_2^1 C_4^4 = 180$(种);
④$a = 0$,$b = 3$,即上下都3次,路径数为$C_6^3 = 20$(种);
所以路径总数为$20 + 180 + 180 + 20 = 400$(种),故蚂蚁移动到原点的概率为$\frac{400}{4^6} = \frac{25}{256}$,故C正确;
对于D,蚂蚁要移动到直线$y = x$上,则水平净移动(向右移动次数减去向左移动次数)要等于垂直净移动(向上移动次数减去向下移动次数)。设水平净移动为$n$,则垂直净移动也为$n$。
当$n = 0$时,水平和垂直净移动均为0,即回到坐标原点,也即C选项所考虑的结果,共400种;
当$n = 1$时,水平和垂直净移动均为1,设向左次数为$l$,则向右次数为$l + 1$;设向下次数为$m$,则向上次数为$m + 1$,总移动次数$l + l + 1 + m + m + 1 = 6 \Rightarrow l + m = 2$,所以可能的组合有:
①$l = 0$,$m = 2$,此时向右1次,向左0次,向上3次,向下2次,路径数为$C_6^1 C_5^0 C_3^3 = 60$(种);
②$l = 1$,$m = 1$,此时向右2次,向左1次,向上2次,向下1次,路径数为$C_6^3 C_3^2 C_1^1 = 180$(种);
③$l = 2$,$m = 0$,此时向右3次,向左2次,向上1次,向下0次,路径数为$C_6^5 C_1^1 C_5^3 = 60$(种);
所以当$n = 1$时,路径总数为$60 + 180 + 60 = 300$种;由对称性,可知当$n = -1$时,路径总数也为300种;
当$n = 2$时,水平和垂直净移动均为2,设向左次数为$l$,则向右次数为$l + 2$;设向下次数为$m$,则向上次数为$m + 2$,总移动次数$l + l + 2 + m + m + 2 = 6 \Rightarrow l + m = 1$,所以可能的组合有:
①$l = 0$,$m = 1$,此时向右2次,向左0次,向上3次,向下1次,路径数为$C_6^2 C_4^0 C_2^3 = 60$(种);
②$l = 1$,$m = 0$,此时向右3次,向左1次,向上2次,向下0次,路径数为$C_6^3 C_3^1 C_2^2 = 60$(种);
所以当$n = 2$时,路径总数为$60 + 60 = 120$种;由对称性,可知当$n = -2$时,路径总数也为120种;
当$n = 3$时,水平和垂直净移动均为3,设向左次数为$l$,则向右次数为$l + 3$;设向下次数为$m$,则向上次数为$m + 3$,总移动次数$l + l + 3 + m + m + 3 = 6 \Rightarrow l = m = 0$,所以可能的组合只有:$l = 0$,$m = 0$,此时向右3次,向左0次,向上3次,向下0次,路径数为$C_6^3 C_3^0 C_3^3 = 20$(种);
由对称性,可知当$n = -3$时,路径总数也为20种;当$n = 4$或绝对值更大时,总移动次数会超过6次,不符合题意。
故蚂蚁移动到直线$y = x$上的总路径数为$400 + 300×2 + 120×2 + 20×2 = 1280$(种),所以概率为$\frac{1280}{4^6} = \frac{5}{16}$。故D正确。故选ACD。
对于B,蚂蚁移动到点$(3,3)$,则需恰好右移3次,上移3次,路径数为$C_6^3 C_3^3 = 20$(种),所以蚂蚁移动到点$(3,3)$的概率为$\frac{20}{4^6} = \frac{5}{1024}$,故B错误;
对于C,要回到原点,则左右移动次数相等,均为$a$次;上下移动次数相等,均为$b$次,总次数满足$2a + 2b = 6$,即$a + b = 3$,可能的组合有:
①$a = 3$,$b = 0$,即左右都3次,路径数为$C_6^3 C_3^0 C_3^3 = 20$(种);
②$a = 2$,$b = 1$,即左右均2次,上下均1次,路径数为$C_6^4 C_4^2 C_2^2 = 180$(种);
③$a = 1$,$b = 2$,即左右均1次,上下均2次,路径数为$C_6^2 C_2^1 C_4^4 = 180$(种);
④$a = 0$,$b = 3$,即上下都3次,路径数为$C_6^3 = 20$(种);
所以路径总数为$20 + 180 + 180 + 20 = 400$(种),故蚂蚁移动到原点的概率为$\frac{400}{4^6} = \frac{25}{256}$,故C正确;
对于D,蚂蚁要移动到直线$y = x$上,则水平净移动(向右移动次数减去向左移动次数)要等于垂直净移动(向上移动次数减去向下移动次数)。设水平净移动为$n$,则垂直净移动也为$n$。
当$n = 0$时,水平和垂直净移动均为0,即回到坐标原点,也即C选项所考虑的结果,共400种;
当$n = 1$时,水平和垂直净移动均为1,设向左次数为$l$,则向右次数为$l + 1$;设向下次数为$m$,则向上次数为$m + 1$,总移动次数$l + l + 1 + m + m + 1 = 6 \Rightarrow l + m = 2$,所以可能的组合有:
①$l = 0$,$m = 2$,此时向右1次,向左0次,向上3次,向下2次,路径数为$C_6^1 C_5^0 C_3^3 = 60$(种);
②$l = 1$,$m = 1$,此时向右2次,向左1次,向上2次,向下1次,路径数为$C_6^3 C_3^2 C_1^1 = 180$(种);
③$l = 2$,$m = 0$,此时向右3次,向左2次,向上1次,向下0次,路径数为$C_6^5 C_1^1 C_5^3 = 60$(种);
所以当$n = 1$时,路径总数为$60 + 180 + 60 = 300$种;由对称性,可知当$n = -1$时,路径总数也为300种;
当$n = 2$时,水平和垂直净移动均为2,设向左次数为$l$,则向右次数为$l + 2$;设向下次数为$m$,则向上次数为$m + 2$,总移动次数$l + l + 2 + m + m + 2 = 6 \Rightarrow l + m = 1$,所以可能的组合有:
①$l = 0$,$m = 1$,此时向右2次,向左0次,向上3次,向下1次,路径数为$C_6^2 C_4^0 C_2^3 = 60$(种);
②$l = 1$,$m = 0$,此时向右3次,向左1次,向上2次,向下0次,路径数为$C_6^3 C_3^1 C_2^2 = 60$(种);
所以当$n = 2$时,路径总数为$60 + 60 = 120$种;由对称性,可知当$n = -2$时,路径总数也为120种;
当$n = 3$时,水平和垂直净移动均为3,设向左次数为$l$,则向右次数为$l + 3$;设向下次数为$m$,则向上次数为$m + 3$,总移动次数$l + l + 3 + m + m + 3 = 6 \Rightarrow l = m = 0$,所以可能的组合只有:$l = 0$,$m = 0$,此时向右3次,向左0次,向上3次,向下0次,路径数为$C_6^3 C_3^0 C_3^3 = 20$(种);
由对称性,可知当$n = -3$时,路径总数也为20种;当$n = 4$或绝对值更大时,总移动次数会超过6次,不符合题意。
故蚂蚁移动到直线$y = x$上的总路径数为$400 + 300×2 + 120×2 + 20×2 = 1280$(种),所以概率为$\frac{1280}{4^6} = \frac{5}{16}$。故D正确。故选ACD。
查看更多完整答案,请扫码查看


